By Hyukpyo Hong, Dae Wook Kim, and Jae Kyoung Kim
Why do genetically identical cells respond differently to the same external stimuli, such as the same antibiotic? To investigate this long-standing question, our research team developed a new framework that analyzes cell reactions to stimuli. We found that cell-to-cell variability in antibiotic stress response increases with the effective length of the cell signaling pathway (i.e., the number of rate-limiting steps). This result can help scientists identify more effective chemotherapies that overcome the fractional killing of cancer cells due to cell-to-cell variability [3].
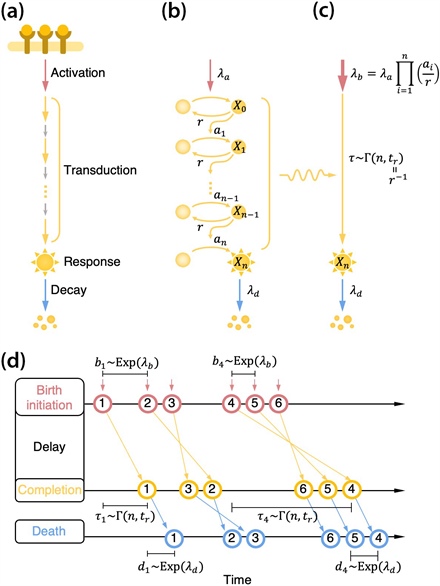
Figure 1. Schematic of the cell signal transduction pathway. 1a. Once an extracellular stimulus activates the signal, the signal is transduced through a chain of intermediate steps and triggers a response (whose intensity then decays). 1b. We can model this process with a chain of reversible activations and deactivations for the conveying molecules. Here, \(\lambda_a\) is the signal activation rate, \(a_i\) is the activation rate of the \(i\)th conveying molecule, \(r\) is the common deactivation rate, and \(\lambda_d\) is the decay rate of the final response. 1c. We can simplify the signal transduction steps via a gamma-distributed time delay \(\tau\) with shape parameter \(n\) and rate parameter \(t_r=r^{-1}\). Here, \(n\) represents the number of rate-limiting steps and \(t_r\) represents the time for each step. 1d. An equivalent queueing process. The inter-event time of birth initiation follows an exponential distribution with rate \(\lambda_b\); following the birth, the process completes with a delay \(\tau\) and disappears after an exponential waiting time with rate \(\lambda_d\). Figure adapted from [3].
Cells in the human body contain signal transduction systems that respond to various external stimuli, such as antibiotics and changes in osmotic pressure. When faced with an external stimulus, sequential biochemical reactions bring about the expression of relevant genes that allow cells to respond to the perturbed external environment. For instance, cells that are exposed to an antibiotic drug may express the relevant antibiotic resistance genes.
The responses of individual cells can vary greatly, even if they receive the same external stimuli [6]. This phenomenon leads to the emergence of persister cells that are highly resistant to drugs [7]. To avoid this problematic situation, researchers must identify the source of such cell-to-cell variability. However, doing so poses a challenge because most intermediate signal transduction reactions are unobservable with current experimental techniques.
To circumvent this limitation, we propose a queueing process that describes a signal transduction system in cells. Specifically, we modeled a chain of reversible activations and deactivations of signaling molecules as a delayed birth-death process (see Figure 1). While the intermediate reactions in the signal transduction system may occur on different timescales, we focused on the few slow steps that limit the reaction rate by determining the time delay of signal transduction. Finally, we use the transient version of Little’s law [1] and the chemical fluctuation theorem [5] to derive an expression for the mean \(\mu(t)\) and variance formula \(\sigma^2(t)\) of the final output signal:
\[\mu(t)=\sigma^2(t)=\frac{\lambda_b}{\lambda_d}\left(\int_{0}^{t}g(\tau;n, t_r)d\tau-\exp(-\lambda_dt)\int_{0}^{t}{g(\tau;n,t_r)\exp(\lambda_d\tau)d\tau}\right).\]
Here, \(\lambda_b\) is the accumulated activation rate, \(\lambda_d\) is the signal decay rate, \(n\) is the number of rate-limiting steps, \(t_r\) is the time for each step, and \(g(\tau;a,b)\) is the probability density function of a gamma distribution with shape parameter \(a\) and scale parameter \(b\).
Based on these expressions, we developed Bayesian inference computational software that we call the moment-based Bayesian inference method (MBI). Users can utilize MBI to analyze the signal transduction system without directly observing the intermediate steps. Our technique accurately and precisely infers parameters in both homogeneous and heterogeneous cell populations.
Figure 2. Our inference method identified a key source of cell-to-cell heterogeneity in response intensity. 2a. The response of various promoters’ fluorescence levels to antibiotics. 2b. Coefficient of variation (CV) of estimated \(\lambda_b\) in a cell population versus the estimated number of rate-limiting steps for various promoters. These quantities have a strong, significant positive correlation (with Pearson correlation coefficient \(\gamma = 0.849\) and p-value \(= 6 \times 10^{-5}\)). Figure adapted from [3].
We applied our method to data from experiments in the literature [4] that measure expression levels of various promoters’ responses to antibiotic stress, such as tetracycline, trimethoprim, and nitrofurantoin in Escherichia coli (see Figure 2a). We estimated the activation rate, decay rate, time for each rate-limiting step of every cell in a colony, and the number of rate-limiting steps for each colony.
Figure 3. In an intracellular signaling pathway, the magnitude of cell-to-cell heterogeneity in the amplified signal activation rate \(\lambda_b\) and signal response intensity both increase when the number of rate-limiting steps in the signaling pathway \(n\) increases. Figure adapted from [3].
Through this approach, we discovered a previously unrecognized parameter that causes cell-to-cell variability: the number of rate-limiting steps in the signal transduction cascade. Specifically, if an antibiotic stress signal is transduced through a pathway with more rate-limiting steps, the variability in the antibiotic efficacy accumulates (see Figures 2b and 3). Our results demonstrate that a larger number of rate-limiting steps between the drug application and therapeutic response increases variability in the drug efficacy.
This important discovery plays a direct role in drug efficacy and provides critical (but previously hidden) information about the selection of target molecules for drug development in a wide variety of settings, such as the treatment of infectious diseases and cancer. Our method can infer the number of rate-limiting steps during signal transduction, which enables the efficient and effective identification of drug targets that show homogeneous therapeutic responses, as well as detection of the source of antibiotic persistence, therapy resistance, and mutation penetrance. Ultimately, this approach facilitates the systematic understanding of heterogeneous treatment effects among patients — a key step toward precision medicine [2].
Hyukpyo Hong presented this research during a contributed presentation at the 2022 SIAM Conference on the Life Sciences (LS22), which took place concurrently with the 2022 SIAM Annual Meeting in Pittsburgh, Pa., last year. He received funding to attend LS22 through a SIAM Student Travel Award. To learn more about Student Travel Awards and submit an application, visit the online page.
References
[1] Bertsimas, D., & Mourtzinou, G. (1997). Transient laws of non-stationary queueing systems and their applications. Queueing Syst., 25, 115-155.
[2] Gewandter, J.S., McDermott, M.P., He, H., Gao, S., Cai, X., Farrar, J.T., … Dworkin, R.H. (2019). Demonstrating heterogeneity of treatment effects among patients: An overlooked but important step toward precision medicine. Clin. Pharmacol. Ther., 106(1), 204-210.
[3] Kim, D.W., Hong, H., & Kim, J.K. (2022). Systematic inference identifies a major source of heterogeneity in cell signaling dynamics: The rate-limiting step number. Sci. Adv., 8(11), eabl4598.
[4] Mitosch, K., Rieckh, G., & Bollenbach, T. (2019). Temporal order and precision of complex stress responses in individual bacteria. Mol. Syst. Biol., 15(2), e8470.
[5] Park, S.J., Song, S., Yang, G.-S., Kim, P.M., Yoon, S., Kim, J.-H., & Sung, J. (2018). The chemical fluctuation theorem governing gene expression. Nat. Commun., 9(1), 297.
[6] Raj, A., & van Oudenaarden, A. (2008). Nature, nurture, or chance: Stochastic gene expression and its consequences. Cell, 135(2), 216-226.
[7] Wakamoto, Y., Dhar, N., Chait, R., Schneider, K., Signorino-Gelo, F., Leibler, S., & McKinney, J.D. (2013). Dynamic persistence of antibiotic-stressed mycobacteria. Science, 339(6115), 91-95.
 |
Hyukpyo Hong is a Ph.D. student in the Department of Mathematical Sciences at the Korea Advanced Institute of Science & Technology (KAIST). His research interests lie in stochastic analysis and Bayesian inference of biochemical reaction networks. |
 |
Dae Wook Kim is a James Van Loo Postdoctoral Fellow and an assistant professor in the Department of Mathematics at the University of Michigan. His research interests lie in the analysis of biological dynamics, development of mathematical frameworks to analyze biological data, and applications to real-world clinical data to ultimately enable personalized circadian medicine. |
 |
Jae Kyoung Kim is an associate professor in the Department of Mathematical Sciences at KAIST and Chief Investigator in the Institute for Basic Science Biomedical Mathematics Group. His research interests lie in biochemical reaction networks and biological oscillators. |