By Paolo Santi
The burgeoning “sharing economy” phenomenon––the collaborative consumption of shared resources made possible by the pervasiveness of information technologies and Internet connectivity [4, 6]––is rapidly taking hold in the context of urban transportation. Business is booming for vehicle-sharing companies, such as Zipcar and Car2Go, and for companies that offer ride-sharing services, such as Bandwagon and Uber, which recently launched the new UberPool application. New sharing services/companies are popping up in cities worldwide.
What are the reasons for this boom? First, urban traffic congestion is a worldwide problem, and it is predicted to become even worse, with an expected tripling in the number of urban trips by 2050 [8]. Second, it is well known that mobility resources are highly underutilized. For instance, most private vehicles lie unused most of the time [3] and typically carry only the driver when in use; in the vast majority of taxi rides, a single passenger is on board [7]. Hence, sharing is considered an effective way of increasing the utilization of mobility resources and, consequently, the efficiency of urban traffic: The higher the vehicle-utilization factor, the lower the number of circulating vehicles, which implies less congestion and pollution.
Despite wide agreement on the potential benefits of the shared economy in urban transportation, quantitative, scientifically accurate studies have been lacking. This is due mostly to two factors: the lack of fine-grained spatial and temporal information about urban mobility patterns, and the immense computational and algorithmic challenges of combining massive numbers of trips at the city scale. As to the former, the big data era is opening the way toward an unprecedented understanding of human mobility at the urban scale [2], which is the prerequisite for the task at hand. As to the latter, the recently introduced notion of shareability networks [5] is a first example of how suitably defined mathematical models can help tame computational and algorithmic challenges.
In a recently-published study [5], we faced the challenge of quantifying the benefits of taxi ride sharing in New York City, starting from a massive data set composed of the more than 150 million trips reported in the city in 2011. A visualization of the trips is available through the HubCab website (hubcab.org) and shown in Figure 1.
|
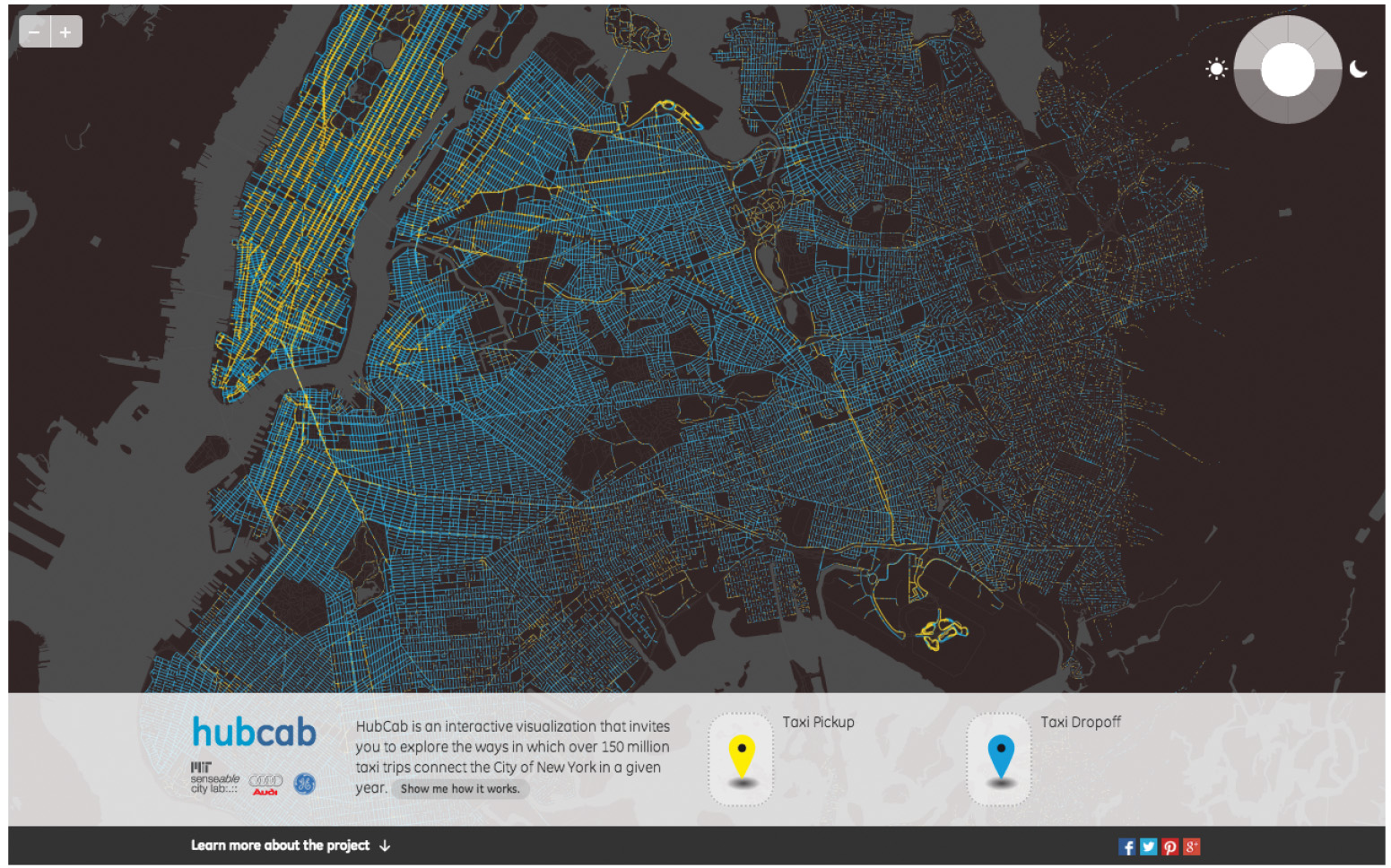
Figure 1. Visualization of the taxi rides in New York City in 2011, with pick-up locations shown in yellow, drop-off locations in blue. Image courtesy of hubcab.org.
|
Traditionally, ride-sharing problems have been approached as an instance of the general class of dynamic pick-up and delivery problems (DPDP) [1], in which items (taxi passengers, in our case) must be picked up from and delivered to specific locations within well-defined time windows, and the goal is to optimize some criterion, such as total distance traveled or number of vehicles used for pick up/delivery. DPDP are typically solved by means of linear programming, and their computational feasibility depends heavily on the number of variables and equations used to describe the problem at hand. This approach is thus unfeasible when applied to problems like city-wide taxi ride sharing, where the potential number of shared trips (roughly corresponding to the number of system variables) is on the order of several thousands or millions.
In [5], we approached the taxi ride-sharing problem in a novel way. The idea was to use combinatorics to impose a structure on an otherwise unstructured, immense search space, as would be explored in traditional linear programming. To structure the search space, we defined two parameters: the shareability parameter \(k\), the maximum number of trips that can be shared, and the delay parameter \(\Delta\), the maximum delay* a customer is willing to tolerate in a shared taxi service. Structuring of the search space, coupled with the notion of shareability networks, as described below, allowed us to find an optimal solution† in an efficient way for an otherwise intractable problem.
Shareability networks are a mathematical model of sharing opportunities. For simplicity, we assume \(k = 2\), and our shareability network is a graph of pair-wise sharing opportunities over all trips. We construct the graph by assigning a node to each trip in the data set, and connecting two nodes with an edge if and only if the trips can be shared. Trip shareability is determined on the basis of the existence of at least one route touching the starting and ending points of both trips,‡ such that both passengers arrive at their destinations with delay at most \(\Delta\). An example of a taxi trip set and corresponding shareability network is shown in Figure 2.
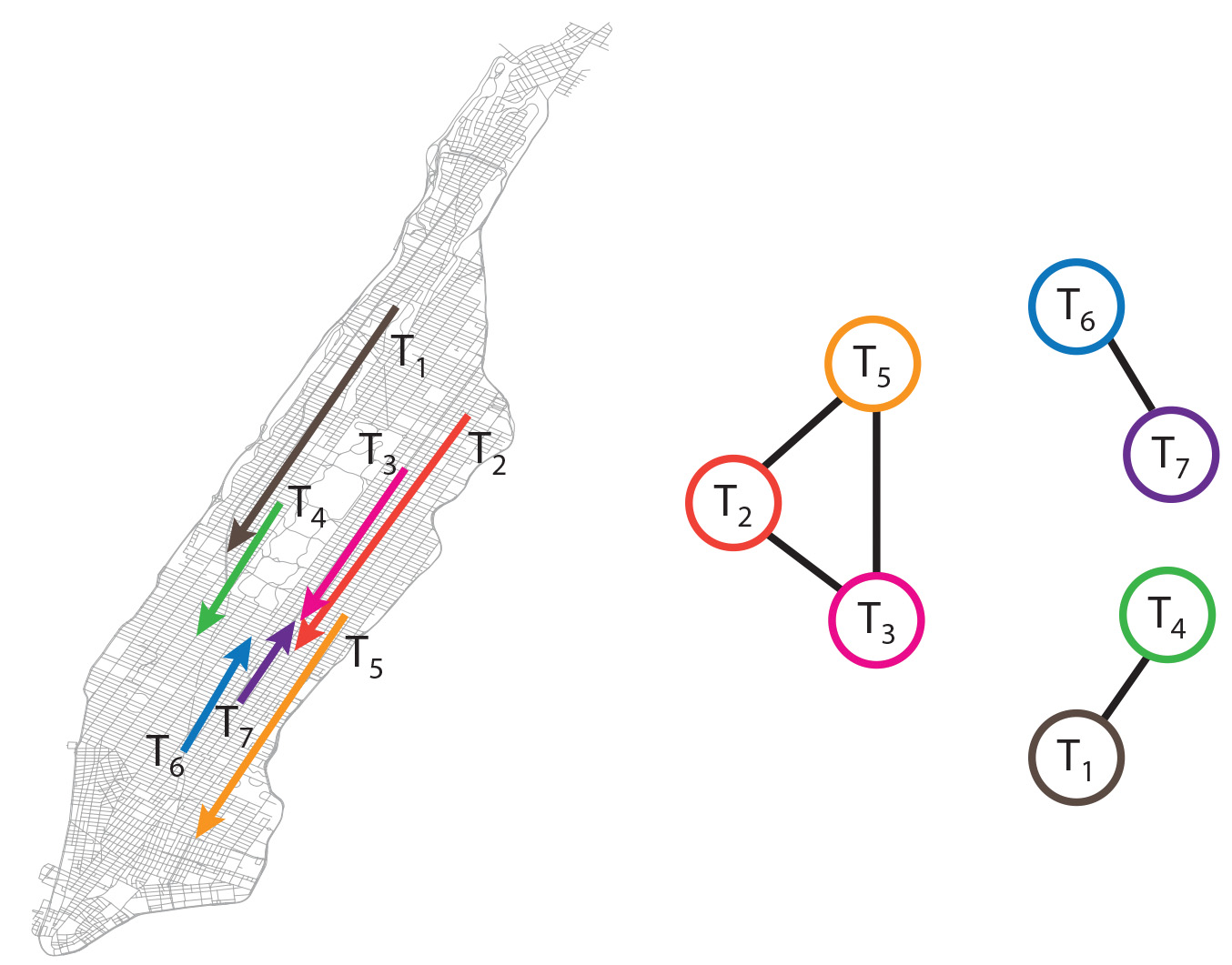
Figure 2. From taxi trips (left) to “shareability networks” (right).
|
Given a shareability network, the problem of optimally matching taxi rides becomes equivalent to the well-known maximum matching problem on graphs, for which efficient solutions exist; this problem formulation allows us to compute the optimal matching of trips across the entire data set of more than 150 million trips. The shareability parameter \(k\) has a major impact on computational complexity: When \(k > 2\), the shareability network becomes a hypergraph, and the problem of computing a maximum matching on the network becomes NP-hard.
The results of our study are extremely encouraging from the sharing economy viewpoint: With \(k = 2\) and a passenger delay of at most 5 minutes, more than 95% of taxi rides in New York can be shared, resulting in a 30% reduction in the total travel time needed to accommodate all taxi requests and, as a consequence, a corresponding decrease in emissions.
The study reported in [5] is only a starting point in the quest for a deeper understanding of the benefits provided by the shared economy of mobility resources, and shareability networks can prove a valuable tool in this endeavor: The main idea, the translation of sharing into graph problems, might prove useful in analyzing other sharing scenarios in tomorrow’s urban mobility landscape.
* Delay is computed as the difference between the estimated arrival times at the destination in the case of a shared trip and in the case of no sharing (single ride).
†The optimality statement holds subject to the above described constraints.
‡Only routes in which both starting points precede the end points are considered.
References
[1] G. Barbeglia, J. Cordeau, and G. Laport, Dynamic pickup and delivery problems, Eur. J. Oper. Res., 202 (2010), 8-15.
[2] M.C. Gonzales, C.A. Hidalgo, and A.-L. Barabasi, Understanding individual human mobility patterns, Nature, 453 (2008), 779-782.
[3] W.J. Mitchell, C.E. Borroni-Bird, and L.D. Burns, Reinventing the Automobile: Personal Urban Transportation for the 21st Century, MIT Press, Cambridge, MA, 2010.
[4] T. Rosenberg, It’s not just nice to share, it’s the future, The New York Times, June 5, 2013.
[5] P. Santi, G. Resta, M. Szell, S. Sobolevsky, S. Strogatz, and C. Ratti, Quantifying the benefits of vehicle pooling with shareability networks, Proc. Natl. Acad. Sci. USA, 111:37 (2014), 13290-13294.
[6] A. Sundararajan, From Zipcar to the sharing economy, Harvard Business Review, January 2013.
[7] New York Taxi and Limousine Commission, 2014 Taxicab Fact Book, 2014.
[8] World Bank, World Development Indicators, 2009; data.worldbank.org/indicator.
Paolo Santi, who currently leads the MIT/Fraunhofer Ambient Mobility initiative at the Senseable City Lab of the Massachusetts Institute of Technology, is a senior researcher at the Istituto di Informatica e Telematica del CNR, Pisa, Italy.