By Oliver G. Ernst and K. Andrew Cliffe
At the first SIAM Conference on Uncertainty Quantification, held in April in Raleigh, North Carolina, a distinguished statistician observed, “UQ—I thought that’s what I had been doing for the past 30 years!” Indeed, one might argue that the origins of mathematical statistics and probability theory, dating back to Laplace and Gauss, were motivated in part by the need to deal with uncertainty from measurement errors.
Three factors have contributed to the explosive growth in the emerging field of modern UQ: an abundance of data resulting from advances in sensor technology, the widespread availability of affordable high-performance computing, and the development and analysis of new algorithms for solving differential equations with random inputs. It is these developments that have enabled the application of UQ techniques to the engineering sciences and other fields, where the point of departure is typically PDE-based modelling of some interesting phenomenon. For many such problems, existing numerical techniques can be used to obtain a solution to essentially any desired accuracy, assuming knowledge of problem inputs, such as the modelling domain, boundary and initial data, coefficients, and source terms. When any of these are uncertain, it becomes necessary to quantify the effect of the uncertainty on the solution of the PDE, or on any quantity of interest, or QoI, derived from the solution. The complete UQ task then consists of determining the uncertainty in the inputs and propagating it to the outputs.
A tried and true approach for approximating statistics of QoIs is Monte Carlo sampling, in which realizations of the random PDE inputs are obtained via random number generators following a postulated probability law. For each generated realization, the QoI is obtained by solution of the resulting deterministic PDE. While simple and robust, MC sampling is plagued by slow convergence, a deficiency that can render it unuseable when the underlying deterministic PDE is computationally expensive. Initiated by the work of Ghanem and Spanos [1] in the early 1990s, new solution techniques, now known as stochastic Galerkin and stochastic collocation methods, have been developed and analyzed by the numerical analysis community; these techniques can exploit smoothness in the dependence of the solution on a (possibly large) number of random parameters to yield algorithms that often outperform MC sampling (see [2] for a survey).
Radioactive waste disposal is an application area in which UQ is a vital instrument for regulatory agencies and other decision-makers. The safe long-term disposal of radioactive waste is an important problem that has implications for the future use of nuclear power. The solution favoured by most countries that have civil nuclear power programs is disposal deep within stable geological formations. The rocks between the repository and the earth’s surface are important in two ways: First, they isolate the waste from the immediate human environment. Second, if radioactive wastes should leak from their containers and escape from the engineered repository, the rocks between the repository and the surface form a barrier that can delay the arrival of harmful radionuclides. If the time for travel from the repository to the surface is sufficiently long, many of the radionuclides will have decayed and the impact, in terms of dose to humans, will have been reduced. This travel time is therefore a crucial parameter in assessing a potential repository.
The basic physics of flow and transport in porous media is reasonably well understood. Because the rock properties cannot be measured everywhere relevant to a calculation, however, uncertainty is inherent in any calculation of travel time. This uncertainty must be represented and its impact quantified as part of a repository assessment. One way to carry out UQ is to use probabilistic methods. We present here a case study in which probabilistic UQ was applied to groundwater flow and radionuclide transport in the assessment of a radioactive waste disposal site, based on data from the site, the Waste Isolation Pilot Plant (WIPP) in Carlsbad, New Mexico.
The primary QoI is the time needed for transport of a radioactive particle by groundwater from the repository to the human environment. The most transmissive feature in the region of WIPP is a thin, but laterally extensive layer called the Culebra Dolomite. Figure 1 shows a cross-section of the geological environment of WIPP. The rocks above and below the Culebra are relatively impermeable. The scenario studied is the release of radionuclides from the repository to the Culebra via a man-made borehole. The mathematical model consists of a stationary two-dimensional diffusion equation, based on Darcy’s law and mass conservation, for the hydraulic head; the hydraulic conductivity is modelled as a random field.
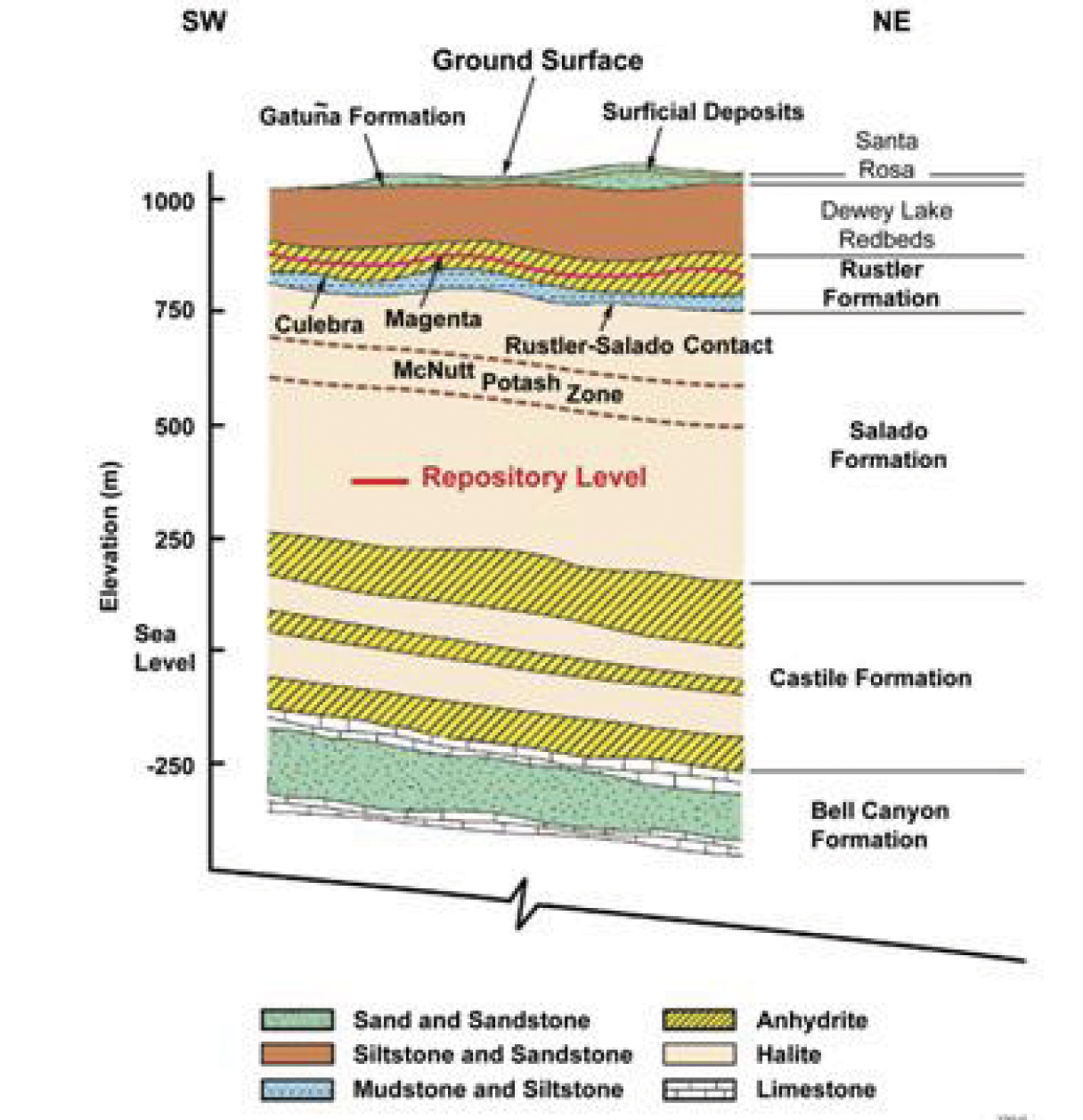
Figure 1. Cross-section of the geological structure surrounding the WIPP repository.
|
Classical geostatistical techniques are used to determine the parameters for the input random field’s probability law. Figure 2 shows the 2D transmissivity field obtained by kriging, a statistical estimation technique based on a set of measurement data. Numerical solutions are obtained with a mixed finite-element discretization of the Darcy flow problem; once the (stochastic) hydraulic head is computed, contaminant transport can be modelled by particle tracing in the associated velocity field.
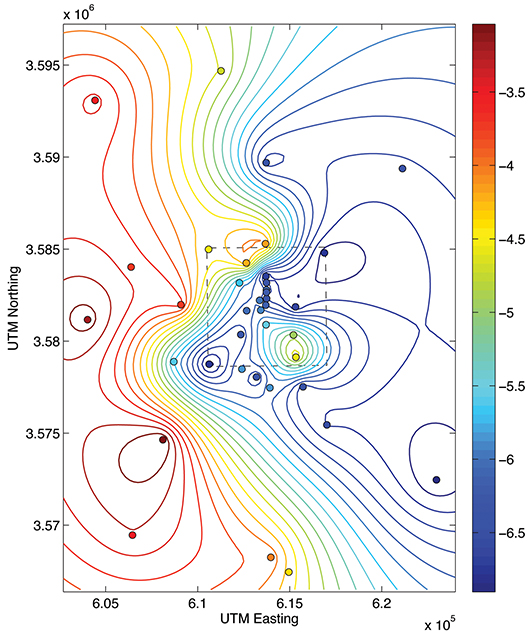
Figure 2. The colored dots indicate the location and value of transmissivity measurements taken in the WIPP area (dashed box) and nearby. The contour lines represent the kriging interpolant used to generate the input of the UQ simulation.
|
In our case study, we compared three approaches: classical brute-force MC simulation, Gaussian process emulators, and stochastic collocation. Gaussian process emulators can provide a stochastic approximation to the output of a computer program as a function of its inputs—in this case the particle travel time is the output, and the parameters determining a finite-dimensional approximation to the random field are the inputs. The third approach involves the numerical solution of the PDE with random data as a parametrized deterministic system. Sparse grid collocation methods are used to discretize the parameter space. This approach is computationally efficient because the spatial problems that have to be solved at each collocation point are independent and the approximation properties of the sparse grid are good.
We calculated the statistical travel time from the stochastic model for each of the methods studied, and compared the results. For a given finite truncation of the random field, the three methods produce very similar results for the cumulative distribution function for travel time. The brute-force MC method is the most expensive, the stochastic collocation method the most efficient.The limitations of methods based on explicit parametrization in terms of random quantities (such as collocation) are encountered when the random fields have very short correlation lengths, as in the rough fields encountered in many geophysical settings. It is often observed, however, that although the solution of the random PDE may have a complicated dependence on a large number of random parameters, certain QoIs lie on a low-dimensional manifold in this parameter space. Much current research in UQ methodology centers on the adaptive capture of this manifold with numerical methods.
References
[1] R. Ghanem and P.D. Spanos, Stochastic Finite Elements: A Spectral Approach, Springer-Verlag, New York, 1991.
[2] C.J. Gittelson and C. Schwab, Sparse tensor discretization of high-dimensional parametric and stochastic PDEs, Acta Numer., 20 (2011), 291–467.
Oliver G. Ernst is a professor of numerical analysis at the Technische Universität Bergakademie Freiberg, Germany. K. Andrew Cliffe is a professor of computational and applied mathematics in the School of Mathematical Sciences at the University of Nottingham, UK.