By Guy Bouchitté, Ornella Mattei, Graeme W. Milton, and Pierre Seppecher
When considering a junction of three or more elements that carry a current, we cannot discern in advance how much current will flow through each element; we only know from Kirchhoff’s law that the sum of the signed currents will equal zero. This is normally an advantage in an electrical circuit, as the current should flow where it is needed. However, it is disadvantageous when someone is trying to protect a circuit from current overloads or surges. Doing so requires nonlinear elements like current limiters, fuses, and surge protectors. For irrigation, this fact is generally unfavorable because water flow is typically rationed between users; this operation also involves the use of nonlinear elements, such as sluice gates or pipes with limited water-carrying capacity.
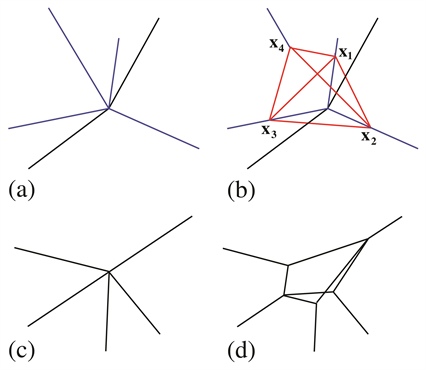
Figure 1. Steps in the replacement of a many-wire junction under balanced tensions, with a network localized around the junction. No more than four wires meet at any junction, and the network still supports the same tensions in the wires that meet it. 1a. One takes any four wires (in blue) that meet the node—which is presumably at the origin—and are such that they do not all lie on one side of a half-plane. 1b. Next, one picks four points on these wires and superimposes a “tensegrity” network that consists of (i) wires under suitable tension (in red) that join the points pairwise and (ii) four rods under balancing compression that connect these four points and the origin. After superposition, a cancellation of tension occurs in one wire that goes to the origin, which one then removes while maintaining a non-negative total tension in the other wires. 1c. This creates three new junctions where five wires meet. 1d. One can then replace each such junction with a web under tension, which has a maximum of four wires at any of the new junctions. One repeats this procedure until the number of wires that meet at the origin is four or less, and then repeats it at every interior node in the network. Figure courtesy of [1].
The situation is completely different for stress. When four stressed wires meet at a node (or at three nodes, if they are coplanar), the tension in one wire determines the tension in the other three due to the balance of forces. By geometry alone, can one achieve a desired guiding of stress in wire or cable networks under tension? In
pentamode metamaterials, exactly four elements meet at the interior nodes; this accounts for their ability to guide stress [3]. Here we focus on finite discrete networks. Structures such as bicycle wheels, suspension bridges, and certain stadiums achieve the desired supporting forces by individually tightening the many spokes or cables and retightening them as needed. In contrast, we aim to create a connected network wherein tightening just one element provides a set of desired supporting forces everywhere. One can achieve this in a simply-connected wire network—where only one (possibly very short) wire is attached to the terminal nodes—by replacing every internal junction where more than four wires meet with a set of junctions, each of which is the meeting point of four or less wires (see Figure 1) [1]. However, applications of this procedure have a significant practical disadvantage: if one wire breaks, the whole network loses its structural integrity, though it may regain its integrity after some finite number of jumps in the points \(\bf{x}\)\(_i\) and changes in the forces \(\bf{f}\)\(_i\) that it supports.
Another important question, which we call the “spider web problem,” is as follows. Given a set of \(n\) balanced forces \(\bf{f}_1, {f}_2, \ldots,\bf{f}\)\(_n\) at \(n\) prescribed points \(\bf{x}_1, {x}_2, \ldots,\bf{x}\)\(_n\), when does there exist a wire network under tension (which can be thought of as a spider web, and possibly have many internal junctions) that supports the forces? It suffices to examine webs when no internal nodes exist, which means that one can easily address the query with linear programming [1]. Going one internal junction at a time, we may inductively replace the wires that are connected to this internal junction with a set of wires that pairwise join the nodes that are connected to the one they are replacing (see Figure 2). In a sense, this is similar to the “star-delta” transformation in resistor networks, though our result only applies to the stress and not to the elastic response of spring networks where one also monitors the displacement. A more powerful argument indicates that the result holds true even if one starts with a continuum of wires [1]. Thus, if one wants a wire network under tension that is as robust as possible to different loadings, then all of this network’s terminals should be connected pairwise. Internal nodes are not needed.
An explicit solution to the spider web problem is available in two dimensions when the points \(\bf{x}_1, {x}_2, \ldots,\bf{x}\)\(_n\) comprise the vertices of a convex polygon [6]. This two-dimensional (2D) case corresponds to the points being coplanar—say, in the horizontal plane—with each \(\bf{f}\)\(_i\) pointing along the plane. A web under tension then exists only if the cumulative torque \(\sum_{k=j}^m (\bf{x}\)\(_k-\bf{x}\)\(_j)\times\bf{f}\)\(_k\) in the upward direction is nonnegative for all \(j\) and \(m\), where the sum is over all points \(\bf{x}\)\(_k\) going clockwise around the boundary from \(\bf{x}\)\(_j\) to \(\bf{x}\)\(_m\) when viewed from above. One can establish this by considering the Airy stress function \(\phi(\bf{x}\)\()\) in the polygon’s interior, denoted \(\Omega\). For smooth stresses \(\sigma(\bf{x}\)\()\) with \(\nabla\cdot\sigma=0\) in \(\Omega\), \(\sigma(\bf{x}\)\() =\bf{R}\)\(_\perp(\nabla\nabla\phi)\bf{R}\)\(_\perp^T\). Here, \(\bf{R}\)\(_\perp\) is the \(2\times 2\) matrix for a 90-degree rotation with transpose \(\bf{R}\)\(_\perp^T=-\bf{R}\)\(_\perp\), and \(\sigma(\bf{x}\)\()\) is positive semidefinite in \(\Omega\) if \(\phi(\bf{x}\)\()\) is convex. For discrete wire networks under tension, this translates to \(\phi(\bf{x}\)\()\) being a convex piecewise linear (piecewise affine) function wherein the wires correspond to its edges and the wires’ tension is related to the jump in \(\nabla\phi\) across the edge [4]. The convexity of \(\phi(\bf{x}\)\()\) translates to this condition on the torques. One can modify \(\phi\) inside \(\Omega\)—and correspondingly change the web—as long as the tangent planes of \(\phi\) just outside the polygon’s boundary remain unchanged. In particular, researchers can take \(\phi\) as the envelope of these tangent planes and find an equivalent web with no internal loops. They can then extend this result to general 2D webs and replace each convex loop with a locally open web. The area of the loops increases with each replacement until only non-convex loops remain, each of which must have an internal force directed inwards at every vertex where the polygon loop points inward. Thus, if \(m\) forces exist in the interior of the convex hull of the points \(\bf{x}_1, {x}_2, \ldots,\bf{x}\)\(_n\), one can replace any web under tension with a web that has at most \(m\) internal loops. A video that demonstrates this process is available online.
Figure 2. Removal of one internal node at \(\bf{x}_0\) that is linked to \(n\) other nodes at \(\bf{x}_1, {x}_2, \ldots,\bf{x}\)\(_n\). If \(T_{0j}\) denotes the tension in the wire from \(\bf{x}_0\) to \(\bf{x}_j\), then one can remove node \(\bf{x}_0\) and replace it with a web in which the surrounding nodes are pairwise connected and have tensions \(T_{ij}=||\bf{x}\)\(_i-\bf{x}\)\(_j||c_ic_j(\sum_k c_k)^{-1}\), where \(c_j=||\bf{x}\)\(_i-\bf{x}\)\(_0||^{-1}T_{0j}\). If a pair of these nodes were already connected, one should add this tension to the existing tension. Here, \(||\bf{x}\)\(||\) denotes the length of \(\bf{x}\). Repeating this procedure allows one to remove all internal nodes. Figure courtesy of [1].
This type of web is less likely to be blocked by the edges of solid objects, such as the corner of a wall that may penetrate the convex hull. In the 2D open webs, where the points \(\bf{x}_1, {x}_2, \ldots,\bf{x}\)\(_n\) are the vertices of a convex polygon, one can move points \(\bf{x}\)\(_i\) backwards and opposite to the direction \(\bf{f}\)\(_i\) while simultaneously maintaining the polygon’s convexity and therefore still satisfying the condition for this web to exist. When points \(\bf{x}\)\(_i\) and \(\bf{x}\)\(_j\) merge, one can replace \(\bf{f}\)\(_i\) and \(\bf{f}\)\(_j\) with \(\bf{f}\)\(_i + \bf{f}\)\(_j\) and continue until just one wire segment supports opposite forces. Retracing the steps provides the open web that supports the original set of forces. Unfortunately, our numerical findings dash the hope that such a procedure may also generate an open web with no closed loops in three dimensions. Initially applying certain forces at a cube’s eight vertices and following the same procedure yields forces at the vertices of a distorted convex cube once the game is up. One is thus at a “stuck” configuration, unable to move any of the points \(\bf{x}\)\(_i\) further in the direction of \(-\bf{f}\)\(_i\) while maintaining the “spider web” condition that supports a web’s existence [1].
Many open problems remain in this area of research. When can one build webs under tension that avoid given obstacles? If building such webs is possible, is there an associated algorithmic procedure? Can one provide a characterization of “stuck” configurations? Can researchers make progress for finite deformations? That is, given moving points \(\bf{x}\)\(_1(t), \bf{x}\)\(_2(t), \ldots,\bf{x}\)\(_n(t)\) and balanced forces \(\bf{f}\)\(_1(t), \bf{f}\)\(_2(t), \ldots,\bf{f}\)\(_n(t)\) that are dependent on time \(t\), when does there exist a single web under tension that supports these forces for some given interval of \(t\)? Here, single web means a web wherein the angles between wires change with \(t\) but the topology and wire lengths do not; all wires also remain under tension and do not collide. Another interesting problem results if some of the wires become slack or collide as \(t\) changes. Can one characterize the possible linear responses of spring networks under tension while also considering displacement at the terminal nodes? Researchers have made a complete characterization without the restriction that all springs are under tension [2]. This leads to a complete characterization of the linear elastodynamic response of mass-spring networks while allowing for internal nodes [5].
Acknowledgments: Ornella Mattei and Graeme Milton are grateful to both the National Science Foundation for support through grant DMS-1814854 and the University of Toulon, where this work was initiated.
References
[1] Bouchitté, G., Mattei, O., Milton, G.W., & Seppecher, P. (2019). On the forces that cable webs under tension can support and how to design cable webs to channel stresses. Proc. Roy. Soc. Lond. Ser. A, 475, 20180781.
[2] Camar-Eddine, M., & Seppecher, P. (2003). Determination of the closure of the set of elasticity functionals. Arch. Ration. Mechan. Anal., 170, 211-245.
[3] Cherkaev, A., Kadic, M., Milton, G.W., & Wegener, M. (2019, June). Pentamode materials: from underwater cloaking to cushioned sneakers. SIAM News, 52(5), p. 1.
[4] Fraternali, F., & Carpentieri, G. (2014). On the correspondence between 2D force networks and polyhedral stress functions. Int. J. Space Struct., 29, 145-159.
[5] Guevara Vasquez, F., Milton, G.W., & Onofrei, D. (2011). Complete characterization and synthesis of the response function of elastodynamic networks. J. Elastic., 102, 31-54.
[6] Milton, G.W. (2017). The set of forces that ideal trusses, or wire webs, under tension can support. Int. J. Solids Struct., 128, 272-281.
Guy Bouchitté is an emeritus professor of mathematics at the University of Toulon. Ornella Mattei is an assistant professor in the Department of Mathematics at San Francisco State University. Graeme Milton is a distinguished professor of mathematics at the University of Utah. He is a SIAM Fellow and recipient of the SIAM Ralph E. Kleinman Prize, among other distinctions. Pierre Seppecher is a professor of mathematics at the University of Toulon.