By Erica Klarreich
Shuckburgh and her colleagues released floats in the Southern Ocean near the estimated hyperbolic points of the flow, and then tracked their paths. “We literally threw them over the back” of the ship, Shuckburgh said at the 2012 SIAM Annual Meeting in Minneapolis. “It was good fun.” Photo courtesy of Emily Shuckburgh, British Antarctic Survey, Natural Environment Research Council.
“The science is clear,” climate scientist Emily Shuckburgh told an audience of nearly 800 people at San Francisco’s Palace of Fine Arts on March 4. “Our collective actions have generated a climate problem that threatens our future and our children’s future.” Shuckburgh’s talk was part of the Mathematics of Planet Earth 2013 Simons Public Lecture Series.*
The combination of mathematical modeling and observational data has created a robust understanding of climate change, as Shuckburgh demonstrated through numerous examples. The results are sobering: Even under the most optimistic assumptions about our future carbon emissions, the planet is already locked into a global temperature increase that will likely reach 2 degrees Celsius over the next century, resulting in increased floods, droughts, and other climate disruptions. And if our carbon emissions continue to grow unchecked, the temperature change will almost surely exceed 4 degrees Celsius, a scenario that, in the words of World Bank president Jim Yong Kim, “can, and must, be avoided.”
In her own research, as head of the Open Oceans group of the British Antarctic Survey, Shuckburgh unites mathematics with field work to tackle one of climate science’s most fundamental challenges: elucidating the interplay between global temperatures and atmospheric carbon dioxide levels. Her work focuses on the Southern Ocean, which plays an outsize role in the exchange of carbon dioxide between the atmosphere and the Earth’s waters.
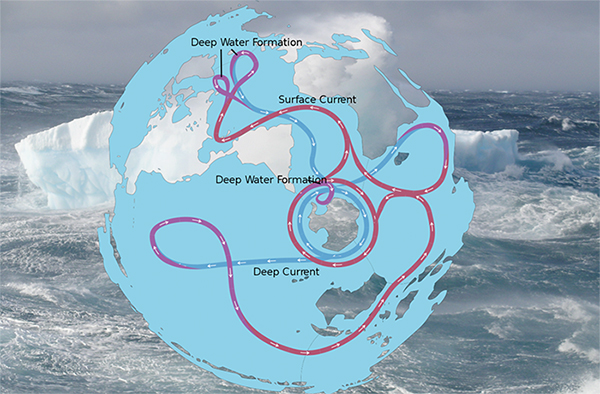
A vast global circulation carries water from the Pacific, Atlantic, and Indian Oceans to the Southern Ocean, allowing water that has been at the bottom of the ocean for centuries to surface and exchange heat and carbon dioxide with the atmosphere. From Creative Commons.
|
Of the carbon dioxide released into the atmosphere through human activities, about half is reabsorbed by land or ocean, protecting the planet from what would otherwise be an even more pronounced greenhouse effect. And of the ocean’s portion of this carbon uptake, 40% occurs in the Southern Ocean. A vast overturning circulation connects all the Earth’s major oceans to the Southern Ocean, carrying water that has been at the bottom of the ocean for many hundreds of years to the surface around Antarctica, where it exchanges heat and carbon with the atmosphere.
When the Earth’s temperature increases, Shuckburgh explained in San Francisco, changes to the ice cover, the temperature of the water, and the overturning circulation of the ocean prompt the release of more carbon dioxide from the Southern Ocean; this increase in greenhouse gases then causes temperatures to increase still further. It’s a feedback effect that we believe has been happening, and that is likely to continue in the future, she said.
Mathematical Model of Ocean Mixing
To fully understand climate change, it is essential to explicate the workings of this “critical gateway for carbon exchange,” Shuckburgh said last summer in a different setting—an invited presentation at the 2012 SIAM Annual Meeting in Minneapolis. What drives the overturning circulation? she asked. And is it likely to change in the future
Derivation of the differential equations governing the ocean’s currents from Newton’s second law is well understood. Computational constraints limit the resolution of the grid on which the equations can be solved, however, and any effects smaller than this resolution can only be estimated. In particular, the grid cannot show the swirling eddy formations that arise from the Earth’s rotation, and these eddies play a major role in the mixing of different ocean waters.
Shuckburgh and her collaborators have created a mathematical model for ocean mixing, including the eddies, using satellite altimetry data, which measures the height—and thus the pressure—of the ocean in different locations. From the pressure, it’s possible to model the surface currents, and thereby examine the dynamics of ocean mixing.
There’s no direct way to measure mixing in the real ocean to see how well the computer model performs. So as a first step toward testing the model, Shuckburgh’s team has used a proxy for the mixing: a dye that the researchers released just west of the Drake Passage between Antarctica and South America in February 2009, and which they have since tracked annually as it flows through the passage.
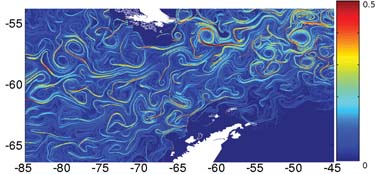
Surface flow through the Drake Passage between South America and Antarctica at one instant in time, as estimated by Shuckburgh’s team from satellite altimetry data. By calculating the flow’s Lyapunov exponents, the researchers were able to home in on the unstable manifolds of this estimated flow. Image courtesy of Emily Shuckburgh, British Antarctic Survey, Natural Environment Research Council.
|
If you stir cream into coffee, the more vigorously you stir, the more complicated the cream formations that initially arise; these formations increase the surface area over which the cream diffuses into the coffee, making the cream assimilate more quickly. In much the same way, when the dye reaches an eddy—whether in computer simulations or in the actual ocean—it swirls into a more complex structure, whose large surface area allows for greater diffusion and increased mixing. Shuckburgh and her collaborators have been tracking the evolution of the dye’s contours in the ocean.
“We’ve sampled it in some locations to see if it has the same structure” as in the computer model, Shuckburgh said. The model “has done remarkably well.”
Dye Maps and Unstable Manifolds
In the computer model, the team released dye in many slightly different locations. As might be expected in a chaotic system, the dye contours that developed over time differed significantly from each other. At the same time, the various dye maps display a structural coherence that is clear to the eye, and is common to all the different releases.
“It’s slightly different in each case, but they’re all falling on the same underlying structure, something related to the flow itself,” Shuckburgh said. “Wherever you put the dye, it’s like an underlying skeleton that the dye maps onto.”
Shuckburgh’s team turned to the theory of dynamical systems to try to elucidate this underlying skeleton. By calculating the velocity field of the surface currents, the researchers were able to identify the hyperbolic points—the fixed points of the flow that attract water along one direction (the stable manifold) and repel it along another (the unstable manifold). And by calculating the stretching rates (the Lyapunov exponents) as nearby points were separated by the flow, the team could determine the direction of maximal stretching—that is, the unstable manifold. It is this manifold that forms the skeleton onto which the dye maps, Shuckburgh said.
“If a blob of dye starts out close to one of the hyperbolic points, it moves toward the point along the stable manifold and then gets pulled out along the unstable manifold,” she said.
To get a better sense of how well the unstable manifolds and Lyapunov exponents estimated from satellite data mirrored the reality in the ocean, Shuckburgh’s team released an assortment of floats in the Southern Ocean near the estimated hyperbolic points, and then tracked the floats’ paths and measured how quickly they separated.
The ship’s crew didn’t quite know what to make of the float releases, Shuckburgh recalled in the Minneapolis talk. “If you’re sitting in the Southern Ocean telling the ship’s captain, who is an old sea dog, that you’re going off looking for unstable manifolds, you might as well tell him you’re looking for the Loch Ness monster,” she said. “They were deeply, deeply skeptical.”
The research team found, however, that the floats do, by and large, follow the unstable manifolds predicted by the satellite data.
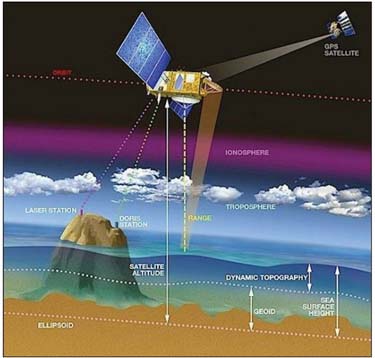
Satellite altimetry measures with great accuracy the height, and thereby the pressure, of the ocean in various locations, enabling Shuckburgh’s team to estimate the surface currents. From Centre National d’Etudes Spatiales.
|
“We’re applying these mathematical ideas well outside the bounds where they’re strictly rigorous, but nevertheless they seem to give us important insights,” Shuckburgh said. “We have reasonable confidence that this is now a good diagnostic of the amount of transport and mixing.”
While the satellite data does a good job of identifying the unstable manifolds in the real ocean, it appears to underestimate the Lyapunov exponents by as much as 50%, presumably because of limitations on the resolution of the satellite data, Shuckburgh said. It may be possible, by releasing floats in additional locations, to figure out whether the exponents derived from satellite data are always off by the same amount, and to make a correction. Or, she said, the solution may simply be to wait a few years until a planned higher-resolution satellite starts to operate.
Science Policy Implications
Even this theoretical work has a direct link to policy decisions, Shuckburgh said, because the amount of carbon dioxide tak-en up by the Southern Ocean is so important for understanding the Earth’s future climate. “There are not many steps between mathematics and policy in a lot of the work we do.”
Shuckburgh dedicates significant time and energy to explaining the policy ramifications of both her own work and other climate research. She has a part-time appointment at the UK Department of Energy and Climate Change, and leads the Climate Science Communications Group at the Royal Meteorological Society. She is a regular speaker at climate change workshops for policy makers and for general audiences.
In her public lecture in San Francisco in March, Shuckburgh painted a grim picture of the planet’s future if we fail to curb carbon emissions, and emphasized that we have years, not decades, in which to come up with solutions to this massive problem. At the same time, she portrayed climate change not just as a threat, but also as an opportunity. “If our collective actions have generated this problem, our collective actions can also help address this problem,” she said.
Shifting her focus to the mathematical sciences community, Shuckburgh points out that “right now, a team is down in the Southern Ocean taking more measurements.” This is just one of the many problems in climate science to which applied mathematicians could bring insight and expertise. “And Mathematics of Planet Earth 2013 will hopefully highlight some of the opportunities and encourage applied mathematicians to get involved.”
*Scheduled to give lectures in the remainder of 2013 are Rupert Klein (Berlin, Germany; May 23); L. Mahadevan (Providence, Rhode Island; September 24); Martin Nowak (Minneapolis; October 8); and Emily Carter (Los Angeles; November 4). Abstracts and illustrations from previous lectures in the series can be found at http://mpe2013.org/public-lectures/mpe2013-simons-public-lecture-series/.
Emily Shuckburgh’s invited talk in Minneapolis can be viewed on the web.
Erica Klarreich is a freelance writer based in Berkeley, California.