By James Case
Power grids, populations, large companies, banking systems, and other collections of numerous and highly interconnected elements are subject to what George Papanicolaou of Stanford University calls “systemic risk.” As he explained in an invited talk at the 2012 SIAM Annual Meeting, each such system is susceptible to a type of “contagion” that, though triggered by seemingly unimportant events, is capable of destroying the whole if allowed to spread unchecked.
Early in the talk, Papanicolaou showed a schematic diagram of the global financial network (see Figure 1). Of course, every country has a financial market of some magnitude, and every such market trades (or can trade) with any other. Many markets and channels, however, are either too small or too faint to show up in a roughly quantitative diagram.
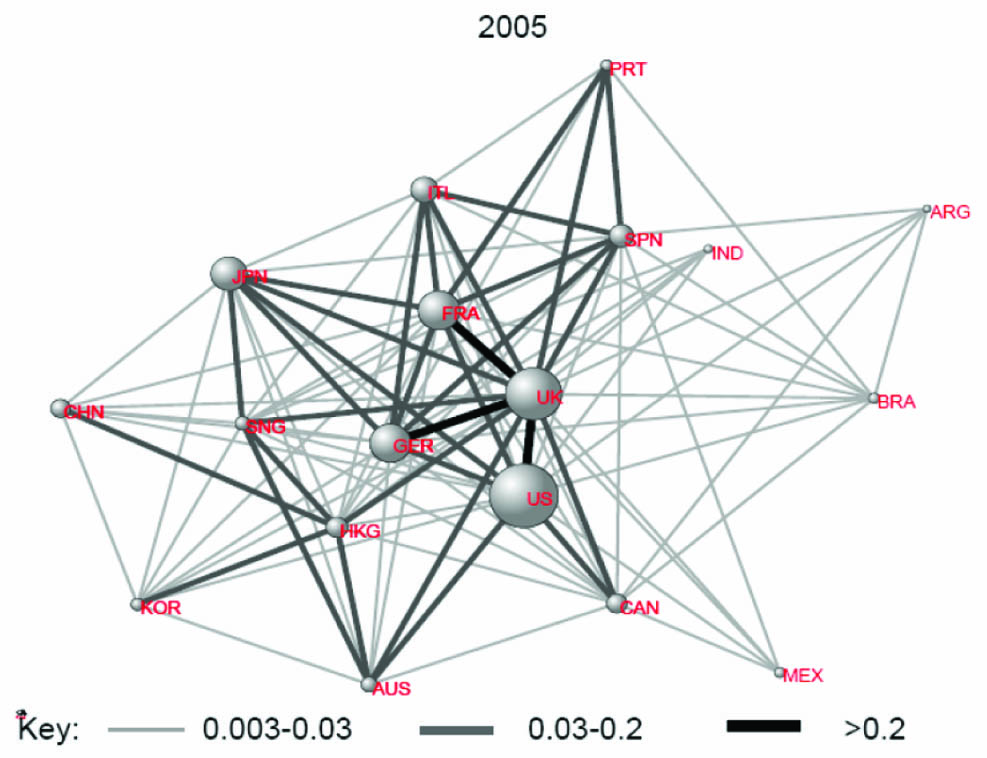
Figure 1. The global financial market in 2005. The sizes of the spheres represent the magnitudes of the corresponding national financial markets, the thicknesses of the connecting edges the volume of traffic between them. From “Rethinking the Financial Network,” a speech given by Andrew G. Haldane, executive director for financial stability, Bank of England, to the Financial Student Association, Amsterdam, April 2009.
|
It is easy to imagine a similar diagram in which the spheres would represent major international banks, and the thickness of the connecting edges would represent the level of (net) indebtedness of one to another. In that case the edges would be directed, and the diagram could be used to assess the risk that the insolvency of even a few of the lesser institutions might spread throughout the global banking system. If the data were sufficiently reliable and up to date, it could even identify the banks best reinforced against the spread of insolvency.
Modeling Systemic Risk
Though the modeling of such systems is in its infancy, Papanicolaou argues that certain existing models, developed for other purposes and subsequently analyzed in depth, shed welcome light on the manner in which local and global risks relate to one another. His exhibit A is an outgrowth of the dynamic Curie–Weiss model, developed long ago for the study of phase transitions in materials and studied in detail during the 1980s. At the heart of the model is a “mean-field interaction” between a (potentially large) number of otherwise independent (scalar) state variables and their arithmetic mean. Considerable work has been done in recent years on mean-field models, in large part because they are particularly amenable to in-depth analysis.
The model Papanicolaou presented consists of \(N\) linked stochastic differential equations involving a potential function \(V\) of a single real variable having just two distinct potential wells. A typical but by no means unique choice would be \(V(y) = ¼y^4– ½y^2\). The equations are
\[\begin{equation} dx_j(t) = –hV´(x_j(t)) ~dt + \theta(\xi(t) –x_j(t)) ~dt + \sigma dw_j(t); j = 1, . . . , N,
\end{equation}\]
where \(\xi = (1/N)\Sigma^{N}_{j = 1}x_j\) is the arithmetic mean of the individual \(x_j\)’s and the \(\{w_j(t)\}^{N}_{j = 1}\) are independent Brownian motions of “strength” \(\sigma > 0\). If \(\theta = \sigma = 0\), the equations reduce to the familiar \(dx/dt = –h ~\mathrm{grad}~ V(x)\), in which \(h\) determines the relaxation time needed to restore equilibrium after a disturbance. If \(\sigma = 0\), the quantities \(x_j(t)\) remain indefinitely in whichever potential well they started; one of the wells represents the normal (solvent, flourishing) state, the other the failed (insolvent, extinct) state. Alternatively, if \(\theta = 0\), the motions are independent. Only if \(\theta > 0\) and \(\sigma > 0\) are there tendencies toward both herd behavior (Papanicolaou calls it cooperation) and randomness, permitting the quantities \(x_j(t)\) to both escape from and return to a particular potential well. The schematic diagram shown in Figure 2 depicts the influences on a single system component \(x_j(t)\).
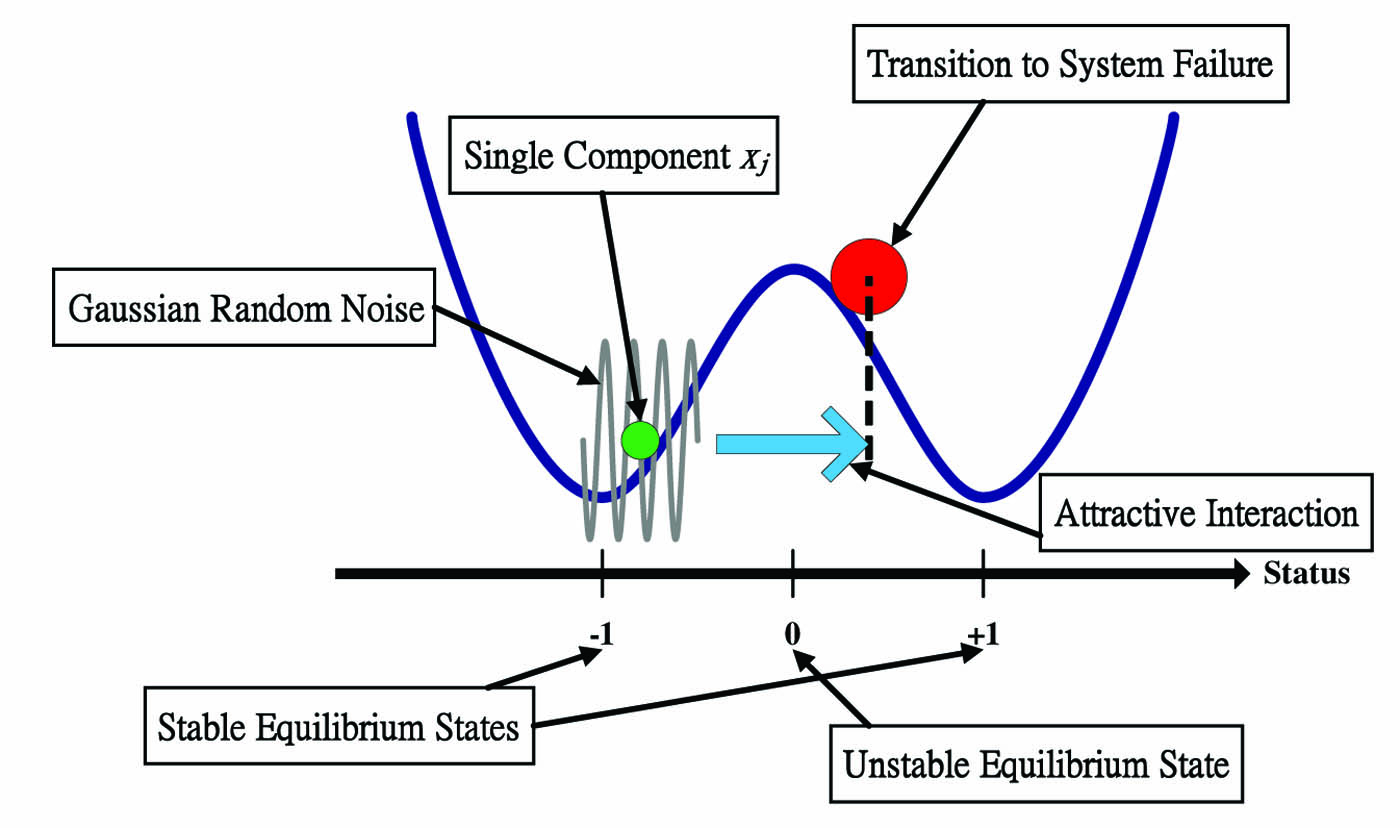
Figure 2. System failure occurs when \(\xi(t)\) migrates from the original potential well (left) to the well on the right.
|
It is known that the empirical risk density \(X_N(t) := (1/N) \Sigma^{N}_{j = 1} \delta_{x_j(t)}(·)\) converges weakly, in probability, as \(N \rightarrow \infty\), to the solution \(u(t,·)\) of a suitable nonlinear Fokker–Planck equation. Loosely speaking, \(u\) can be regarded as the probability density of a random variable \(X_{\infty}(t)\) representing the centroid of an infinite population of points on a line. It can then be shown that, given \(h\) and \(\theta\), there exists a critical value \(\sigma_c\) such that \(u\) exhibits one stable equilibrium if \(\sigma \geq \sigma_c\) and two if \(\sigma < \sigma_c\). Furthermore, if \(h\) is small, \(u\) can have two stable equilibria only if the herding instinct dominates noise to the extent that \(3\sigma^2 < 2\theta\).
For \(V(y) = ¼y^4 – ½y^2\), additional concrete results can be obtained by linearizing the differential equations about \(x_j(0) = –1 \forall_j\), the \(N + 1\) linearized variables being \(\delta x_j\) and \(\delta\xi\). If they all vanish at \(t = 0\), then \(\delta x_j(t)\) and \(\delta\xi(t)\) are Gaussian processes of zero mean and readily calculable variance, provided that the ratios \(\sigma^2/N\) and \(\sigma^2/2(\theta + 2h)\) remain small enough for the linearizations to remain valid. All this reveals that (i) a stronger herding instinct (larger \(\theta\)) leads each herd member to believe that it can survive more violent shocks (larger \(\sigma\)), and (ii) the effects of their own actions on the overall system are invisible to other herd members.
Under additional hypotheses, it is possible to estimate (in closed form) the risk that the system will fail in the precise sense that \(\xi(t)\) transitions from the healthy potential well to the unhealthy one. The resulting expression justifies the conclusions that (i) a large system is more stable than a small one; (ii) sooner or later, the dread transition will take place; (iii) any increase in the intrinsic stabilization parameter \(h\) reduces the risk of systemic transition; and (iv) a stronger herding instinct (larger \(\theta\), with \(\sigma^2/\theta\) held fixed) increases systemic risk.
High-speed Trading
Having pretty well exhausted the potential of his modified Curie–Weiss model, Papanicolaou turned his attention to empirical studies of the real or imagined effects of “algorithmic trading” on market performance. Estimating that some 70% of all equities trading is currently algorithmic, he observed that over the last 10–15 years, the automation of exchanges, and the increasing use of high-speed, computer-driven algorithmic trading schemes—capable of assessing and electronically executing trades in mere fractions of a second—has spurred the development of new strategies that “execute trades based on complex and sophisticated trading signals.” Focusing on just three macroscopic properties of financial markets—their liquidity, their volatility, and their diversity—he summarized efforts to understand their combined effects on systemic risk.
The volatility of market indices is a familiar quantity, usually measured by the variance of day-to-day price increments. Liquidity is a more elusive quantity, inasmuch as it refers to the amount of cash or cash equivalents (aka liquid assets) available to traders for the purpose of making purchases, and is not directly observable. It is necessary, therefore, to develop “proxies” for liquidity, perhaps the most obvious being the commissions paid to brokers (who are not traders) for executing individual trades. The commissions reduce market liquidity by decreasing the amount of money available for additional trades. There is little doubt that the advent of electronic trading has decreased brokers’ commissions dramatically.
Figure 3. The number of independently migrating asset groups (eigenvectors of the price-series correlation matrix) is inversely related to the volatility of the market, as measured by the published VIX statistic.
The bid/ask spread on traded assets is another natural measure of liquidity: When the price would-be buyers are willing pay for a given asset differs little from the price would-be sellers are willing to accept, the volume of trade in that asset tends to increase, much as it would if traders had extra money to spend. Traders thus consider markets to be particularly liquid when the bid/ask spreads are unusually small. All told, Papanicolaou presented six measures of market liquidity, all of which tend to support the theses that volatility and liquidity are strongly and positively correlated, and that algorithmic trading has increased market liquidity in recent years.
With a particularly intriguing slide (see Figure 3), Papanicolaou compared the volatility of the S&P 500 index (as measured by the published VIX statistic) for the years from 1992 to 2008 with the number of significant eigenvalues of the empirical covariance matrix of the 500 individual stock price series. Each such eigenvector represents a group of issues that tend to move together, independently of other groups, making it possible to construct “diversified” portfolios—consisting of a single issue from each of several independent groups—that combine low risk with high reward. During the 1990s, when the VIX was consistently low, there were seldom fewer than forty such independently moving groups. But following the dot-com crisis of March 2000, and again during the financial crisis that began in 2008, the number of such groups dipped into the low single digits even as volatility soared, making low-risk/high-reward portfolios all but impossible to construct.
Papanicolaou concluded with the observation that investors are generally suspicious of reduced transaction costs and increased liquidity. Many would favor a “Tobin tax,” which would impede the flow of transactions by taxing them. Europeans, he said, are generally in favor of such measures, while the “free market” ideologues in Washington and on Wall Street are unalterably opposed. With or without such a tax, difficult questions will remain concerning the command and control of systemic risk. Who, Papanicolaou wondered, will perform the basic research necessary to answer such questions? Traders aren’t interested—they’re too busy making money. The banks aren’t interested—they get bailed out whenever they fall prey to risk of any kind. The regulators express interest but lack the necessary resources and know-how. Only academics, in his opinion, possess both the will and the skill to answer such questions.
James Case writes from Baltimore, Maryland.