By Tamar Schlick
Progress in science depends on new techniques, new discoveries and new ideas, probably in that order. -- Sidney Brenner (2002 Nobel laureate in physiology or medicine)
It was an exciting day for the fields of computational chemistry and biology when news of the 2013 Nobel Prize in Chemistry filtered in early on the morning of October 9, 2013. Awarded to Martin Karplus, Michael Levitt, and Arieh Warshel for the “development of multiscale models for complex chemical systems,” the prize provided a welcome “seal of approval” to a field that historically struggled behind experiment. This is not unlike the traditional division between pure and applied mathematics, stemming from the difference between using exact theories to solve ideal problems versus approximating complex physical systems to solve real problems. Historically, the results of simulations for biological and chemical systems were judged by their ability to reproduce experimental data. Thus, computational predictions had to pass the scrutiny of experimentalists, who employ direct, though not error-free, measurements, especially for large systems. If results from computations agreed with experiment, they were considered uninformative, but if they predicted properties ahead of experiment, they were considered unverifiable and hence unpublishable!
In time, however, just as applied mathematics and computational science evolved into huge successful fields in their own right, computations in chemistry and biology are finally recognized not only as valid for making predictions and generating insights into physical systems, but as necessary for addressing complex problems we face in the 21st century. In fact, clever modeling ideas and methods for the design of appropriate algorithms are essential for discovering the information missing from products of current high-throughput technologies; this is because genome sequencing, microarrays, and other technologies and instrumentation produce voluminous amounts of genomic sequences and related data for systems whose structures, functions, and interactions are largely unknown.
This is not the first time the Nobel committee celebrated computations. In 1998, the Nobel Prize in Chemistry was awarded to Walter Kohn for the development of density-functional theory, and to John Pople for the development of computational techniques and the pioneering program GAUSSIAN for quantum chemistry calculations. But this year’s prize-winning contributions are more general and perhaps more far-reaching. The separate work of the three laureates, and their interactions with each other and with others in the community, offer an opportunity to examine the history of the field and view how people, ideas, and technologies come together to shift existing paradigms. The prize also provides an exceptional occasion to look into the bright future of a field whose three powerful arms—physical experimentation, theory, and computer simulation—can lead to the solution of key problems ranging from the workings of individual proteins to the packaging of DNA, DNA repair and RNA editing processes, and interactions among and within cells, organs, and organisms (Figure 1).
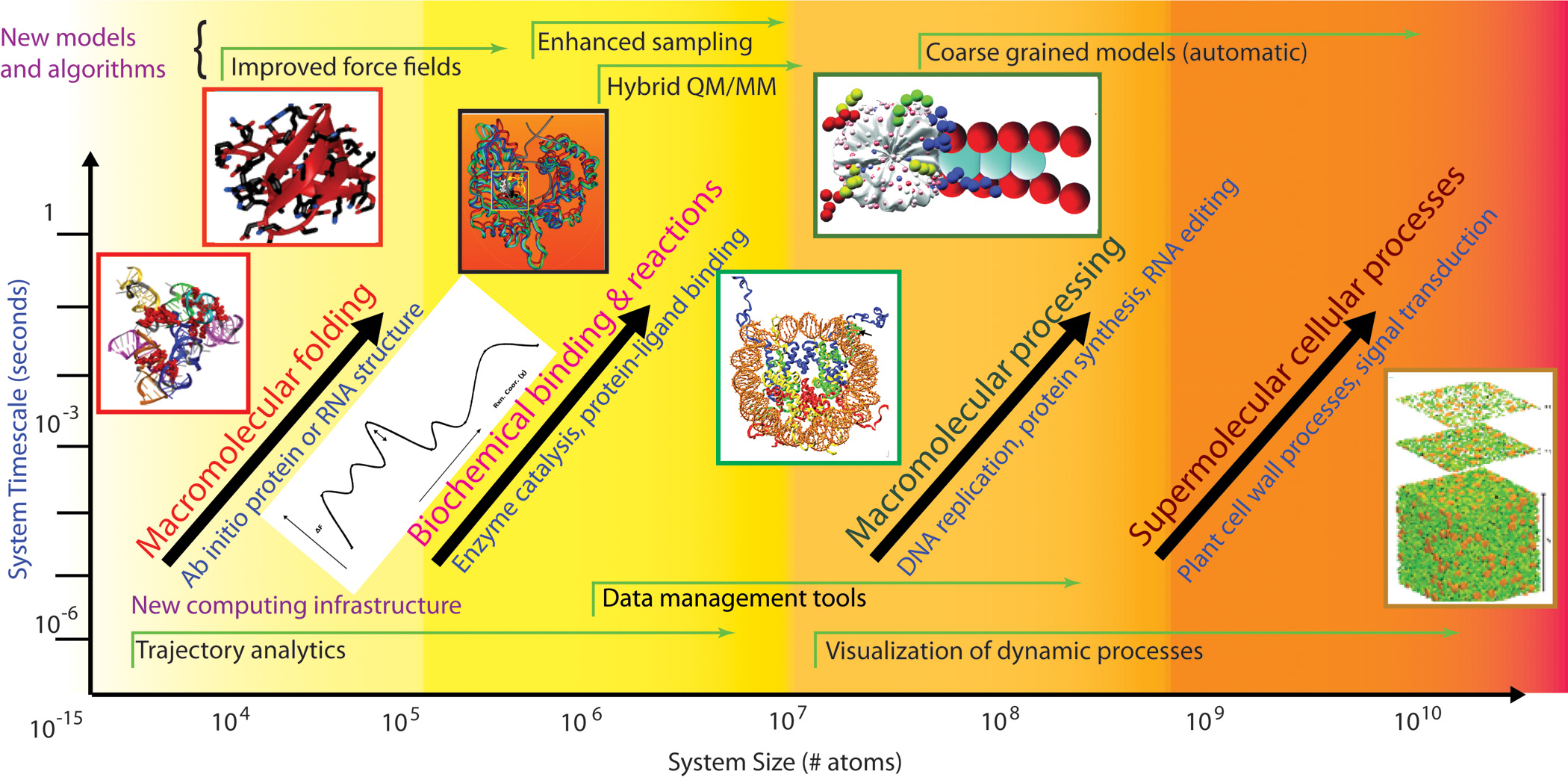
Figure 1. Vision for the future of the field of molecular modeling. Adapted from a figure developed by the author and members of a DOE study panel [23].
|
Field Trajectory
The roots of molecular modeling reside with the notion that molecular geometry, energy, and many related properties can be calculated from mechanical-like models subject to basic physical forces. These molecular mechanics concepts of molecular bonding and van der Waals and electrostatic forces arose naturally from quantum chemistry theory developed in the 1920s, leading to several different Nobel Prizes in Physics: to Bohr, de Broglie, Dirac, Heisenberg, Planck, and Schrödinger. In particular, quantum chemistry led to the Born–Oppenheimer approximation, in which atomic nuclei can be considered fixed on the time scale of electronic motion. Quantum chemistry was also the basis of Linus Pauling’s fundamental research on the nature of the chemical bond and its application to the elucidation of the structure of biological molecules, as recognized by the 1954 Nobel Prize in Chemistry. In fact, ahead of his time, and relying in part on quantum chemistry (concepts of orbital hybridization, ionic bonds, and aromatic compounds) mastered during his earlier studies with Bohr and Schrödinger, Pauling correctly predicted a planar peptide bond in 1951. Based on this notion, he used paper cutouts to predict the α-helix and β-sheet as the primary structural motifs in protein secondary structure. Watson and Crick used wire models around that time to deduce the structure of DNA. While the first molecular mechanics calculations, notably of Frank Westheimer, date to the 1940s, computers were not yet available for practical applications. Other early contributors to molecular modeling include Kenneth Pitzer and James Hendrickson, as highlighted in [5].
In the early 1960s, work on the development of systematic force fields began independently in three laboratories around the world. These pioneers were the late Shneior Lifson of the Weizmann Institute of Science, Harold Scheraga of Cornell University, and Norman Allinger of Wayne State University and later the University of Georgia. At Weizmann, a second-generation computer was already available to the researchers, called Golem for a powerful but soul-less hero in Jewish folklore. Scheraga and Allinger used a CDC-1604 computer and an IBM 360/65 machine, respectively, in those early days.
With their talented co-workers—notably Némethy with Scheraga, Warshel, who was Lifson’s graduate student, and Levitt, who came to Lifson at Weizmann with a Royal Society fellowship—the groups pursued the arduous task of selecting functional forms and parameters for bonded and nonbonded interactions from spectroscopic information, heats of formation, structures of small compounds, other experimental data, and quantum-mechanical information. Importantly, hydrogen bonds were expressed by simple electrostatic interactions. A comparison of calculated structures and energies for families of compounds composed of the same basic chemical subgroups with experimental observations led to an iterative process of force-field refinement. The three resulting empirical force fields—consistent force field (CFF) [13], empirical conformational energy program for peptides (ECEPP) [15], and the molecular mechanics family MM1, MM2, . . . [2] formed the basis for numerous programs and applications in the decades to come.
While the Lifson/Warshel and Allinger schools used energy minimization to calculate molecular properties, Scheraga and co-workers pursued the ideas of statistical mechanics to generate conformational ensembles of molecules that approach the statistically correct Boltzmann distribution. These concepts are now prevalent in modern Monte Carlo and molecular dynamics simulations. Scheraga also combined his expertise in experimental physical chemistry with theory in very early investigations of many biological problems, such as protein stability and folding pathways [19].
In their pioneering Cartesian coordinate CFF treatment [13], Levitt, Lifson, and Warshel calculated energies, forces (first derivatives), and curvature (Hessian) information for the empirical potential function. Levitt and Lifson soon reported the first energy calculation of entire protein molecules (myoglobin and lysozyme) [11]; they used not only the empirical potentials but also experimental constraints to guide the minimization, by the steepest descent method. Levitt and Warshel later followed with a pioneering coarse-grained protein simulation [12], with atoms grouped into larger units and normal modes used to escape from local minima. Levitt and the late Tony Jack of Cambridge also pursued the idea of using molecular mechanics force fields with energy minimization as a tool for refining crystal structures [7]. Konnert (in 1976) and Hendrickson (from 1980) extensively developed macromolecular crystal refinement [6], based on methods of Waser (from 1963).
More than two decades later, minimization with constraints or restraints has become a practical and widely used tool for refining experimental diffraction data from X-ray crystallography, by optimization and, more effectively, by simulated annealing and molecular dynamics [3]. (I had the good fortune to work with Lifson as a postdoctoral fellow in 1989 for a few months during an NSF mathematical sciences postdoc at the Courant Institute. I recall Lifson proudly noting that his students took his “small ideas” and applied them to much larger systems, notably biomolecules.)
In 1969 Karplus, Levitt, and Warshel intersected in Lifson’s lab at Weizmann. Karplus, on sabbatical from Harvard, sought inspiration from Lifson’s mastery of polymer theory and broad thinking and hoped to marry his own interests in theoretical chemistry with biology [8]. Having been Pauling’s graduate student at Caltech, Karplus already had a deep interest in the structure of biological molecules. At Weizmann, further inspiration came from Lifson’s visitor Chris Anfinsen, whose experiments in protein folding prompted Karplus and David Weaver to develop, in 1975, a diffusion–collision model for protein folding calculations [8].
This intersection of broad thinkers at Weizmann in the late 1960s also led to Warshel’s postdoctoral position with Karplus at Harvard. Karplus had been working on reaction kinetics problems, specifically electronic absorption theory, and with students and postdocs (Barry Honig and, later, Klaus Schulten and others) calculated structural changes from electronic excitation related to the photo-isomerization reaction (e.g., retinal molecule) [8]. Warshel continued this line of work by constructing a program for computing vibrational and electronic energy states of planar molecules [25]. To achieve this, Warshel and Karplus used a novel combination: classical-mechanics approximation based on CFF with a quantum-mechanical Hamiltonian correction [25]. Four years later, Warshel and Levitt described a general hybrid classical/quantum scheme, not restricted to planar molecules for which the separation between quantum and classical degrees of freedom is clear [26] (Figure 2). The two reunited in Cambridge, UK, where Levitt received his PhD at the Medical Research Council under the tutelage of John Kendrew and Max Perutz, whose 1962 Nobel Prize in Chemistry recognized “their studies of the structures of globular proteins”; Levitt continued to pursue his interests in computational biology there [10]. These hybrid classical/quantum methods, essential for studying reactions in which bond breaking/formation occurs, use quantum mechanics to model a small active site, with classical mechanics for the larger region, beyond the reactive site (Figure 2). In this way, the overall computational time can be made manageable. Today, many innovative thinkers work in the huge area of computational/theoretical chemistry concerned with modeling details for the quantum region, and especially for the boundary between the two regions.
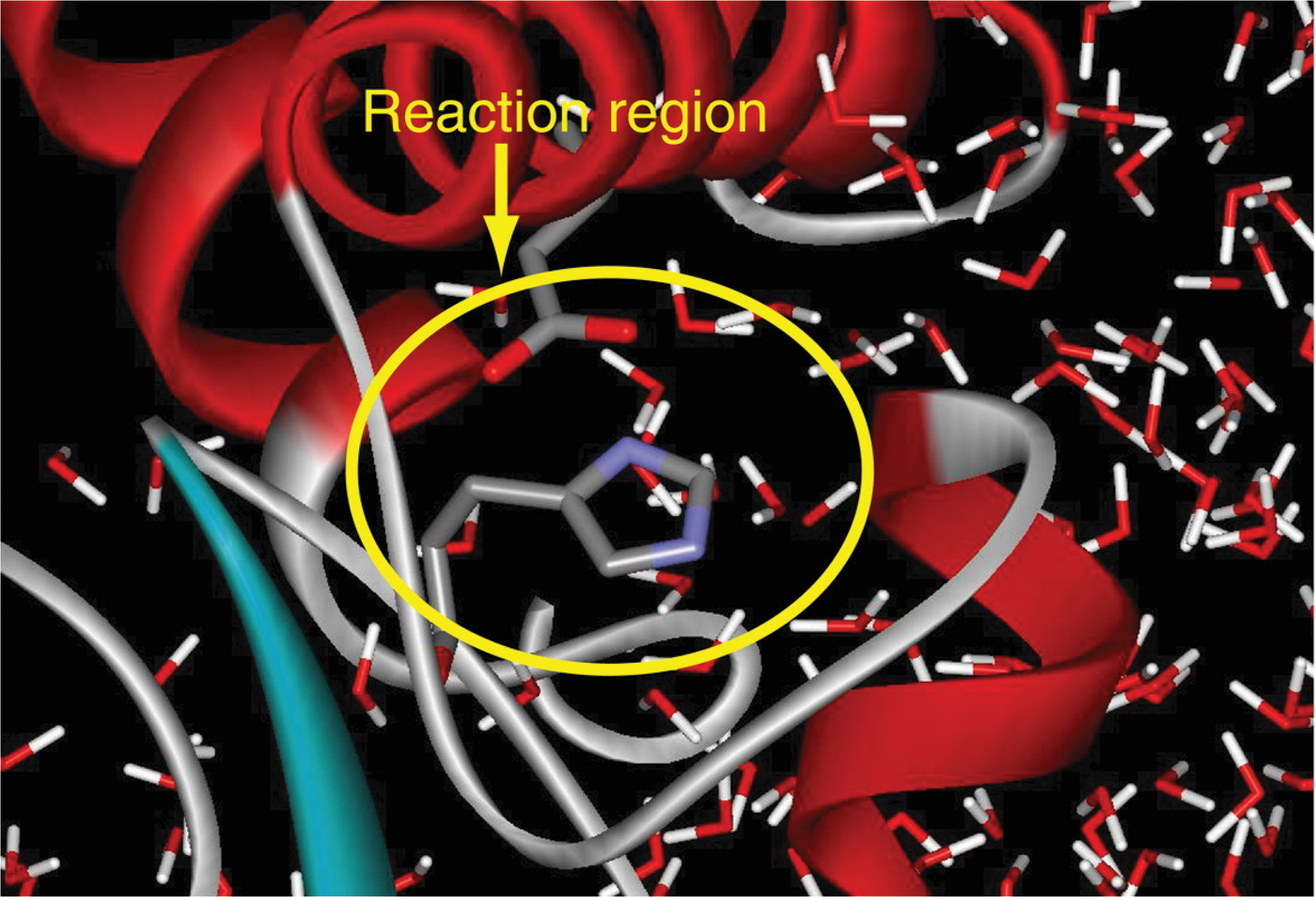
Figure 2. With hybrid MM/QM methods, a small reaction region is treated quantum mechanically, while the surrounding solvent and remaining biomolecular system is treated classically. Figure courtesy of Arieh Warshel.
|
Activities under way at this time also led to other pioneering molecular dynamics simulations. Building on the simulation technique described in 1959 by Alder and Wainwright but applied to hard spheres [1], Rahman and Stillinger reported the first molecular dynamics work on a polar molecule, liquid water [18]. Again, computer power was not sufficient for realistic simulations, and the idea did not catch on quickly. In the late 1970s, Warshel brought his and Levitt’s CFF program to the Karplus lab, where, rewritten by Karplus’s graduate student Bruce Gelin, it formed the basis for second-generation programs, including CHARMM at Harvard and AMBER from Peter Kollman’s group at UCSF.
A spectacular application of CHARMM was the first simulation of protein dynamics, by Andrew McCammon with Gelin and Karplus in 1977 [14]. Although modeled in a vacuum, with a crude molecular mechanics potential, and covering only 9.2 ps (tiniest “building” in Figure 3), the results emphasized the advantage of the dynamic view compared to the static, time-averaged X-ray image. Though these early simulation results stood the test of time, realistic molecular dynamics simulations generally require the inclusion of solvent (water) and ions in the physical environment. This necessitated the further creation of water force fields, which were developed by Berendsen, Jorgensen, and others in the late 1970s and early 1980s. These advances and the advent of supercomputers in the mid- to late 1980s led to molecular dynamics simulations of biomolecular systems, resulting in numerous exciting discoveries about the systems.
The vision of another giant in the field, the late Peter Kollman, led to the application of force-field methodology and computer simulation to biomedical problems, such as enzyme catalysis and protein/ligand design [24]; his group’s free energy methods, combined quantum/molecular mechanics applications, and contacts with industry opened many new doors for practical pharmaceutical applications of molecular modeling.
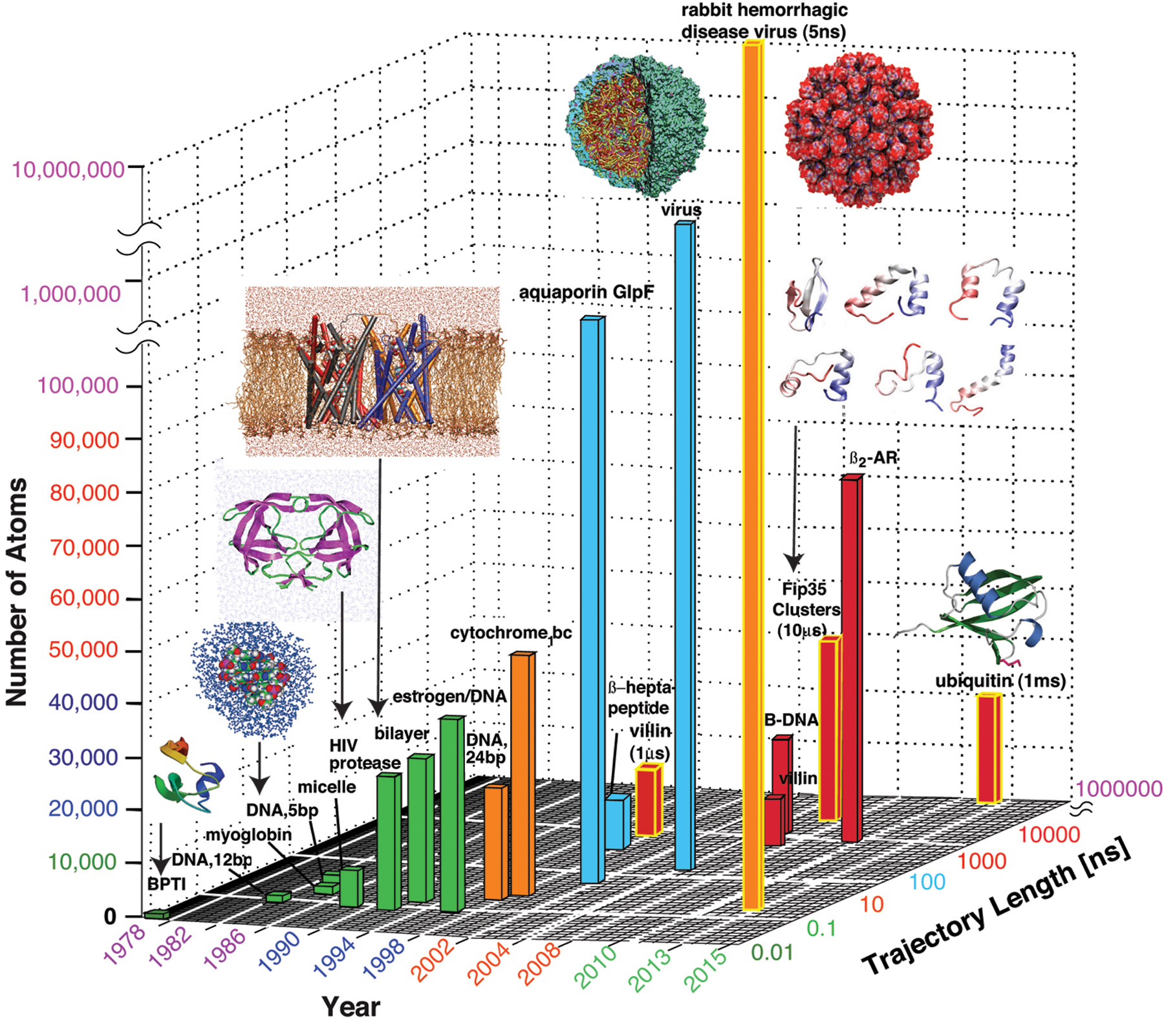
Figure 3. The evolution of molecular dynamics simulations with respect to system sizes and simulation times. The “buildings” are colored according to simulation duration. See text and [20] for details.
|
Critical Assessment
The new field of computational structural biology faced exciting yet difficult times as it matured and expanded to many new areas of application. En route, it capitalized on the growing capabilities of high-speed computers. Initially, the pioneers were not widely supported, partly because their work could not easily be classified under a traditional label like physical or organic chemistry. At the same time, experimentalists were quite curious about the predictions produced by molecular modeling and simulations. As described in our earlier field perspective article [22] and a related SIAM News article [21], the new capabilities made possible by supercomputers in the late 1980s also led to inflated expectations and unrealistic predictions that temporarily harmed the field. Reports of various triumphs were followed in the media by extrapolated projections that computational tools would soon supplant experimentation and lead to novel computer-designed drugs (see quotes in [22]).
But a determined focus by modelers on two major limitations of biomolecular computations—imperfect force fields and limited conformational sampling—resulted in many improvements and refinements. In fact, in [22] we used historical facts to create a “field expectation” curve showing that, despite early exaggerated expectations, the field rebounded around 2000 and moved onto a productive trajectory, working hand-in-hand with experiment [22]. Thus, this year’s Nobel Prize celebrates the ability of simulations not only to survive critical assessment by experimentalists, as described in 2005 [9], but to thrive as a field in its own right. Self-critique is also an important feature of the field: Several collective exercises, carefully distinguished from competitions—in protein structure prediction, RNA structure prediction, and other important applications—have served to assess progress and guide future developments in the field.
A Productive Present
Today, several popular biomolecular simulation packages are adapted to the latest computational platforms, as biomolecular modelers take advantage of the explosion of accessible technology and the tremendous increases in computing memory and speed. For example, the free and open-source software NAMD, developed at the University of Illinois at Urbana–Champaign by Schulten and co-workers, can be adapted to many force fields and computer architectures [16]. A specialized computer for long molecular dynamics simulations developed at D.E. Shaw Research is also available through a national supercomputer center. Such programs, along with technological advances, have led to important milestones.
Figure 3 shows representative advances in molecular system sizes and timescales over several decades, including the early landmark simulations discussed above. In 1998 the 1-µs folding simulation of a small protein required four months of dedicated Cray computing [4]. In 2010 and again this year, the 1-ms simulation of a small protein [17] was made possible by Anton, the D.E. Shaw computer. At the same time, impressive developments in computer speed and memory have made possible simulations of extraordinary sizes, such as the 5-ns simulation of a virus system of more than 64 million atoms this year [27].
We have come a long way from the computers of the early days, Golem, CDC-1604, IBM-360, and their predecessors, with their tiny memories, low floating-point performance, limited compilers, and cumbersome physical requirements (e.g., magnetic tape, punch cards). Today, successful applications to biology and medicine are routinely reported, and mathematicians and computational scientists are the contributors of many important ideas and methods, including symplectic integrators, particle-mesh Ewald methods for electrostatic computations, and Markov state models for sampling (details can be found in [20]). Recent successes include structure predictions that precede experiment, protein folding theories, and modeling-aided drug discovery and design. Other important achievements involve successful interpretation of experimental structures, especially resolution of experimental contradictions, as well as production of new hypotheses for biological and chemical systems, which ultimately can be tested [22].
A Bright Future
Looking ahead, it is clear that multiscale modeling approaches like those devised by this year’s Nobel laureates will be needed to describe biological processes on many levels (see Figure 1). The physical problems extend beyond the folding of individual biomolecules to the understanding of enzymatic reactions and binding processes, pathways that involve proteins and nucleic acids (e.g., DNA replication and RNA editing), and processes on cellular scales, like cell signaling, cellular metabolism, tumor growth, and neural circuitry. All these applications will require continuous development of methods and infrastructure support for data analysis and visualization. Ultimately, techniques for automatic coarse-graining of biological models could serve as a telescope focused on the region of interest: By adjusting both spatial and temporal domains, we might some day be able to focus the calculation on the process of interest at the desired scale, whether it occurs on the level of a single molecule or an entire organism. Needless to say, technological advances, together with a multidisciplinary community of scientists who have a broad vision, will be required to meet the important challenges in biology and medicine we now face.
Acknowledgments: I thank Namhee Kim and Shereef Elmetwaly for assistance with the figures and Wilma Olson, Ned Seeman, and Shulamith Schlick for insightful comments on a draft of this article.
References
[1] B.J. Alder and T.E. Wainwright, Studies in molecular dynamics, I: General method, J. Chem. Phys., 31 (1959), 459–466.
[2] N.L. Allinger, M.A. Miller, F.A. Van-Catledge, and J.A. Hirsch, Conformational analysis, LVII: The calculation of the conformational structures of hydrocarbons by the Westheimer–Hendrickson–Wiberg method, J. Amer. Chem. Soc., 89 (1967), 4345–4357.
[3] A.T. Brünger, J. Kuriyan, and M. Karplus, Crystallographic R factor refinement by molecular dynamics, Science, 235 (1987), 458–460.
[4] Y. Duan and P.A. Kollman, Pathways to a protein folding intermediate observed in a 1-microsecond simulation in aqueous solution, Science, 282 (1998), 740–744.
[5] J.B. Hendrickson, Molecular geometry, I: Machine computation of the common rings, J. Amer. Chem. Soc., 83 (1961), 4537–4547.
[6] W.A. Hendrickson, Stereochemically restrained refinement of macromolecular structures, Meth. Enzymol., 115 (1985), 252–270.
[7] A. Jack and M. Levitt, Refinement of large structures by simultaneous minimization of energy and R factor, Acta Crystallogr., A34 (1978), 931–935.
[8] M. Karplus, Spinach on the ceiling: A theoretical chemist’s return to biology, Ann. Rev. Biophys. Biomol. Struc., 35 (2006), 1–47.
[9] M. Karplus and J. Kuriyan, Molecular dynamics and protein function, Proc. Natl. Acad. Sci. USA, 102 (2005), 6679–6685.
[10] M. Levitt, The birth of computational structural biology, Nat. Struc. Biol., 8 (2001), 392–393.
[11] M. Levitt and S. Lifson, Refinement of protein conformations using a macromolecular energy minimization procedure, J. Mol. Biol., 46 (1969), 269–279.
[12] M. Levitt and A. Warshel, Computer simulation of protein folding, Nature, 253 (1975), 694–698.
[13] S. Lifson and A. Warshel, Consistent force field for calculations of conformations, vibrational spectra, and enthalpies of cycloalkane and n-alkane molecules, J. Chem. Phys., 49 (1968), 5116–5129.
[14] J.A. McCammon, B.R. Gelin, and M. Karplus, Dynamics of folded proteins, Nature, 267 (1977), 585–590.
[15] G. Némethy and H.A. Scheraga, Theoretical determination of sterically allowed conformations of a polypeptide chain by a computer method, Biopolymers, 3 (1965), 155–184.
[16] J.C. Phillips et al., Scalable molecular dynamics with NAMD, J. Comput. Chem., 26 (2005), 1781–1802.
[17] S. Piana, K. Lindorff-Larsen, and D.E. Shaw, Atomic-level description of ubiquitin folding, Proc. Natl. Acad. Sci. USA, 110 (2013), 5915–5920.
[18] A. Rahman and F.H. Stillinger, Molecular dynamics study of liquid water, J. Chem. Phys., 55 (1971), 3336–3359.
[19] H.A. Scheraga, Respice, adspice, prospice, Ann. Rev. Biophys., 40 (2011), 1–39.
[20] T. Schlick, Molecular Modeling: An Interdisciplinary Guide, 2nd ed., Springer-Verlag, New York, 2010.
[21] T. Schlick and R. Collepardo-Guevara, Biomolecular modeling and simulation: The productive trajectory of a field, SIAM News, 44:6 (2011), 1 and 8.
[22] T. Schlick, R. Collepardo-Guevara, L.A. Halvorsen, S. Jung, and X. Xiao, Biomolecular modeling and simulation: A field coming of age, Quart. Rev. Biophys., 44 (2011), 191–228.
[23] Scientific grand challenges: Opportunities in biology at the extreme scale of computing, Workshop Rep., August 2009; http://science.energy.gov/~/media/ascr/pdf/program-documents/docs/Biology_report.pdf.
[24] W. Wang, O. Donini, C.M. Reyes, and P.A. Kollman, Biomolecular simulations: Recent developments in force fields, simulations of enzyme catalysis, protein–ligand, protein–protein, and protein–nucleic acid noncovalent interactions, Ann. Rev. Biophys. Biomol. Struc., 30 (2001), 211–243.
[25] A. Warshel and M. Karplus, Calculation of ground and excited state potential surfaces of conjugated molecules, I: Formulation and parametrization, J. Amer. Chem. Soc., 94 (1972), 5612–5625.
[26] A. Warshel and M. Levitt, Theoretical studies of enzymic reactions: Dielectric, electrostatic and steric stabilization of carbonium ion in the reaction of lysozyme, J. Mol. Biol., 103 (1976), 227–249.
[27] G. Zhao et al., Mature HIV-1 capsid structure by cryo-electron microscopy and all-atom molecular dynamics, Nature, 497 (2013), 643–646.
Tamar Schlick ([email protected]) is a professor of chemistry, mathematics, and computer science at New York University.