By Dana Mackenzie
Imagine cellular factories churning out biofuels. Nanomachines hunting out cancer cells. Machines growing from living tissues. These were some of the visions proposed at the start of the new millennium by the founders of a subject they called synthetic biology. It was like genetic engineering but more ambitious: Instead of merely splicing a single gene from one organism into another, synthetic biologists would design entire new biological circuits from scratch.
Fourteen years later the revolution is still going on, but with tempered expectations. Living cells have proved to be more unpredictable than electric circuits. In waves of hype and anti-hype, synthetic biology has been portrayed as either a visionary technology or a bust.
One thing, though, has remained constant. Since its inception, synthetic biology has embraced mathematics in an attempt to fast-forward past the tinkering stage to the engineering stage. “You need something that goes beyond intuitive understanding, something that is quantitative. Only mathematical models can really provide that,” says Krešimir Josić, a mathematician at the University of Houston. While the equations might look familiar, biology has a way of putting a new twist on some classical problems of circuit design and electrical engineering.
Mathematical Beginnings
In the late 1990s, James Collins of Boston University, along with then-graduate student Tim Gardner, set out to “forward engineer” genetic circuits. At the time, the Human Genome Project was turning up many new gene networks inside human cells. Biologists were trying to reverse engineer some of those networks to figure out what they did and how they did it.
Collins, who was trained as a physicist, thought it made more sense to go in the other direction. He proposed to forward engineer simple gene networks whose function is known and whose behavior is predictable. For anyone with a background in computer science or electrical engineering, the benefits of such an approach are obvious. Every computer is designed from innumerable small parts—switches, logic gates, timers. Why not build biological systems the same way? The information gleaned in the engineering of synthetic parts could also help biologists understand natural networks.
At a key moment in his and Gardner’s work, Collins says, former SIAM president Martin Golubitsky, current director of the Mathematical Biosciences Institute at Ohio State University, visited their lab for a yearlong sabbatical. “He encouraged us to think about the simplest mathematical models possible,” Collins says. Before you can run, you have to walk. And before you can walk, you have to be able to switch a cell on and off.
In the end, Collins and Gardner focused on one of the simplest systems possible—a genetic toggle switch, comprising two genes. “Each one has a promoter, a strip of DNA that’s basically an on switch for the gene,” Collins explains. “You engineer it so that the protein produced by gene A wants to bind to the on switch for gene B and turn it off, and vice versa.”
The system can be modeled with two differential equations, analogous to the equations describing two competing species. It’s a well-known theorem that under many conditions, one species (or in this case, one gene) will win. If it is to behave as a switch, the system needs to have two stable equilibria, one with gene A on and gene B off, the other with gene B on and gene A off. It also needs a chemical trigger that will move it from one equilibrium state to the other.
“What surprised us was how hard it was experimentally to find regions of bistability,” Collins says. “Our mathematical models and our biological understanding are not as good as we thought, and not as good as they should be to do predictive design.”
Collins’s team introduced a gene into the human intestinal bacterium E. coli that would enable it to produce a green fluorescent light; they also put in a DNA switch that would turn the fluorescent protein on and off. After nine months and plenty of false starts, the system finally worked. Their paper was published in Nature in 2000, right next to a paper by a Princeton University team, Michael Elowitz and Stanislas Leibler, who had engineered a simple oscillating circuit in the same bacterium. The two papers are still universally cited as the starting point for synthetic biology.
But several not-so-obvious problems would slow progress in the field. Electrical circuits can be wired up from off-the-shelf parts that work together in a predictable way. This is still far from the case for gene circuits. “Pretty much every sophisticated circuit that was published in Nature or Science probably took four or five years to assemble, fine tune, and test,” says Domitilla Del Vecchio, a dynamical systems theorist at MIT. The Princeton group’s oscillator is not robust—it often fails to work, depending on conditions in the cell. As for Collins’s switch, it works qualitatively the way the equations predict, but “in a quantitative way it’s far away,” Josić says. By now, hundreds of simple gene circuits have been produced, but many of them have the same problems—they are poorly documented and finicky, and the models describing them are inaccurate.
Another problem that has become increasingly evident is what synthetic biologists call “context-dependent behavior.” Gene networks may work differently, or not at all, in different cells. And different genetic circuits can interfere with each other. Engineers are used to the fact that electrical circuits are modular: Different components either do not interfere with one another, or they interact in predictable ways. So far, the jury is out on whether biological systems can be coaxed into working the same way. “Synthetic biology is a test of how modular biology really is,” says Pamela Silver, a systems biologist at Harvard University.
Mathematical Cures for Biological Ills?
Much as mathematics helped synthetic biology get started, it also may help the field overcome some of its growing pains. Two recent examples suggest how synthetic biology can live up to its name and become a synthesis of biology and math.
The Biological Amp. In her research with biologist Alex Ninfa of the University of Michigan, and more recently with biological engineer Ron Weiss of MIT, Del Vecchio has studied a context-dependent behavior called retroactivity. This occurs when a “downstream” system affects an “upstream” system. For example, you might introduce a gene network into the cell that produces an oscillating signal. Then you might add a counter and a switch to tell the cell to release a certain protein after a certain number of oscillations. Alas, as soon as you connect up these components, the oscillator stops working. Because the counter and the switch do not receive the oscillating signal, the protein is not released. What happened?
The problem is well known in engineering. The downstream components, often called the “load,” might use a chemical that the upstream circuit needs to produce its oscillations. Electrical engineers solve the problem by introducing a third device, such as an isolation amplifier, that insulates the oscillator from the load while still allowing it to transmit the signal to the load. The isolation amplifier uses negative feedback. When it detects a deviation from the desired signal, it adds a compensating signal to counteract the error. Often, it needs to amplify the compensating signal.
“When I saw that this standard negative feedback design would help with the loading effect, I asked Alex if he knew any biological system that would implement the idea,” Del Vecchio recalls. “He immediately said, ‘Phosphorylation.’” This is a chain reaction that is the cell’s natural method for amplifying signals. By adding a phosphorylation cascade to her circuit, Del Vecchio isolated the upstream oscillating module from the load, making the whole system work again.
“That circuit is now a submodule of a bigger system I’m working on with Ron Weiss, to control the level of beta cells in the pancreas,” Del Vecchio says. The dream application would be to engineer pancreas cells to self-medicate, in order to treat diabetes. But, she emphasizes, that’s a long way off. “Honestly, we’re just starting to build all the parts. If you ask me in five years, I hope to tell you we’re close to getting the circuit to work.”
A Matter of Timing. As Del Vecchio’s example suggests, both organisms and machines need reliable ways to keep time. In the ordinary world, clocks require a steady oscillator, such as a pendulum or a quartz crystal. The same is true at the cellular level. Unfortunately, genetic oscillators depend on chemical reactions, and chemical reactions speed up when the temperature rises. The molecular clock therefore speeds up as well.
This year, in the Proceedings of the National Academy of Sciences, Josić, along with mathematician William Ott of the University of Houston and physicist-turned-biologist Matthew Bennett of Rice University, described the first synthetic genetic clock that compensates for temperature changes. The discovery began with an improved mathematical model of the oscillator (see Figure 1.) Ordinary differential equations ignore the time that it takes for a bacterium like E. coli to transcribe its DNA into RNA and to translate the RNA blueprint into proteins. “It’s not like electric circuitry, where signals go at the speed of light,” Ott says. “There are always lags.” A more accurate model would involve delay differential equations.
|
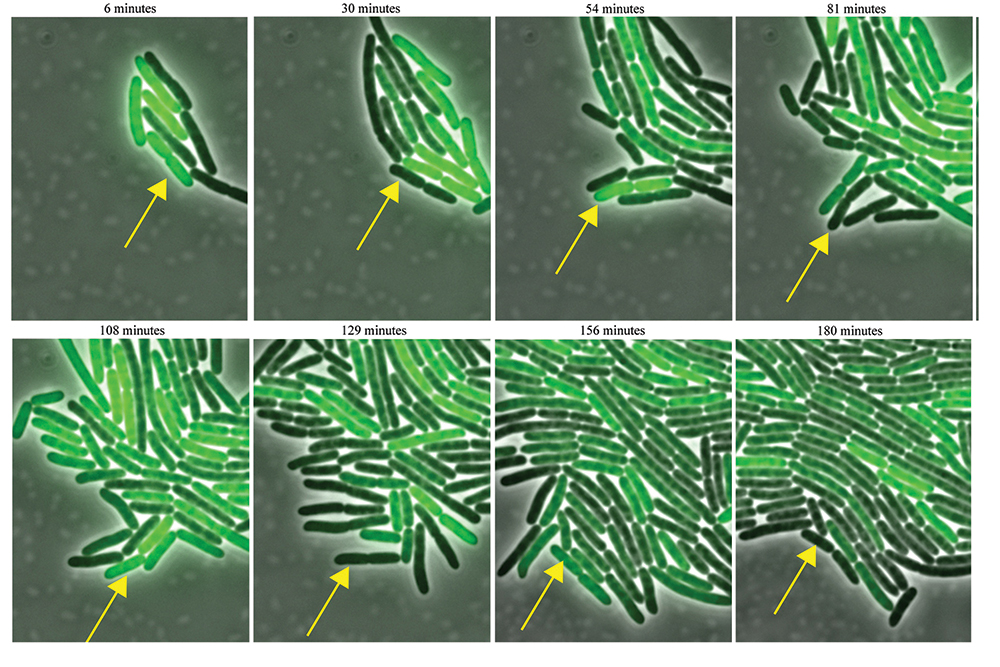 Figure 1. An E. coli bacterium (arrow) equipped with a synthetic genetic circuit blinks on and off, as the circuit activates and deactivates a green fluorescent protein. A mathematical model helped to predict a mutation that keeps the genetic clock running at a steady tempo, independent of temperature. Image courtesy of the Bennett Lab, Rice University. Figure 1. An E. coli bacterium (arrow) equipped with a synthetic genetic circuit blinks on and off, as the circuit activates and deactivates a green fluorescent protein. A mathematical model helped to predict a mutation that keeps the genetic clock running at a steady tempo, independent of temperature. Image courtesy of the Bennett Lab, Rice University.
|
Bennett had a general theoretical idea of how temperature compensation could work, and the model gave them more specific ideas of the kind of intervention they needed. We decided to make a point mutation,” Ott says. In particular, they wanted a mutation that would “repress the ability of the repressor to repress.”
The back-and-forth between biology and mathematics continued. Bennett suggested several known mutations that were believed to make an inhibitor bind less effectively to its target as the temperature goes up. According to the mathematical model, this could neatly compensate for the increased reaction rates. And, in fact, when they introduced one of the mutations, the oscillator kept steady time over a 10-degree (Celsius) range of temperatures.
Josić emphasizes that they still don’t have experimental proof that the mutation affects the inhibitor in the way that the model suggests. The model can only propose a mechanism. The other plausible mutations didn’t work, moreover, which means that true predictive engineering is still a work in progress. “We have shown that temperature compensation can be achieved, but that’s not the same as saying you can exactly control it and exactly understand what is happening,” Ott says.
In both of these cases, mathematicians and biologists complemented each others’ strengths. “We as engineers can write equations and do the mathematics, but when it comes to implementing these things, the collaborations have been instrumental,” says Del Vecchio.
Synthetic biology will certainly continue to be a good source of math problems. Control theory might improve biological circuits that are too finicky to work autonomously. There is some evidence that engineered cell communities behave more dependably than engineered networks of genes. These “cellular consortia” display new behaviors, such as pattern formation, and involve partial differential equations to track how chemicals diffuse and how cells move through space. Some may even require agent-based models to track individual cells.
Finally, cells do one thing that no electrical engineer ever had to worry about: They divide. What happens to a green blinking bacterium when it splits into two bacteria? As Ott says, “The number of interesting problems is large, and they are different from the types of problems that come from within math.”
Dana Mackenzie writes from Santa Cruz, California.