By Anupam Sengupta, Francesco Carrara, and Roman Stocker
Phytoplankton are photosynthetic microorganisms that form the base of most aquatic food webs, impact global biogeochemical cycles, and produce half of the world’s oxygen. Many species of phytoplankton are motile and migrate through the water column via gravitaxis, directional movement in response to gravity. They move upward toward light during the day and downward toward higher inorganic nutrient concentrations at night [7]. Despite the minute size of individual organisms, phytoplankton’s immense numbers make these migrations some of the largest and most important on Earth. Understanding how physicochemical cues from the environment—such as light, nutrients, and turbulence—affect migration greatly impacts our ability to predict the diel vertical migration of phytoplankton. This type of migration contributes significantly to the biological pump, the process driving carbon sequestration from the atmosphere to the deep ocean through sinking particulate organic matter [1].
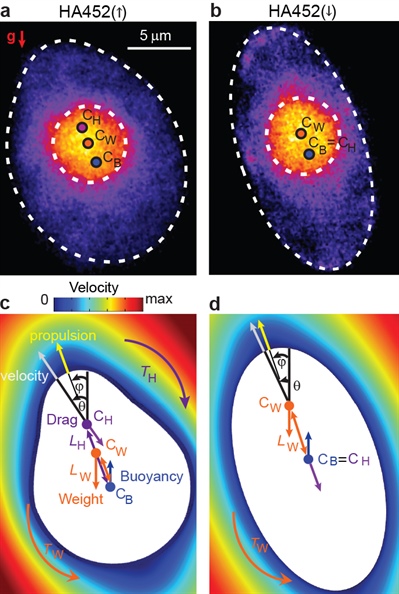
Figure 1. A change in morphology underpins the emergence of a downward swimming subpopulation in Heterosigma akashiwo strain HA452. 1a and 1b. False-color epifluorescence micrographs of upward swimming—HA452(↑)—and downward swimming—HA452(↓)—subpopulations. White dashed lines denote the contour of the cell body and nucleus (bright orange). CW, CB, and CH are the centers of mass, buoyancy, and hydrodynamic stress, respectively. 1c. and 1d. Free body diagrams showing the forces acting on the cell overlaid on the numerically-computed flow field around the cell (not to scale). 1c. HA452 cells swimming upwards after exposure to turbulent cues for 30 minutes are top-heavy (CW above CB) and fore-aft asymmetric (CH above CB); thus, TW and TH act in opposition. 1d. HA452 cells swimming downwards after exposure to turbulent cues for 30 minutes are fore-aft symmetric (CH coincides with CB and thus TH vanishes) and top-heavy (CW above CB), so that TW causes cells to orient downwards. Adapted from [8].
Ramon Margalef, one of the founding fathers of modern marine biology, was among the first to recognize the fundamental role of turbulence in phytoplankton ecology [6]. Strong turbulence can be detrimental to phytoplankton, as it has the potential to cause flagellar or body wall damage, increased physiological stress, and reduced growth [10]. To cope with environmental stressors such as turbulence and yield adaptive strategies, phytoplankton exploit the intrinsic plasticity of their functional traits [9]. For instance, over the course of several hours in regions of strong turbulence, the dinoflagellate
Ceratocorys horrida reduces the length of its spines to enhance sinking [11], presumably down to calmer ocean layers, while
Alexandrium catenella forms chains to alter swimming behavior as an active response to hydrodynamic shear [4]. However, while scientists have long recognized that turbulence is a primary determinant of plankton fitness and succession, it is unclear whether phytoplankton can actively respond to turbulence over behavioral timescales. Given that turbulent disturbances can be highly localized and intermittent [5], it is possible that phytoplankton evolved avoidance mechanisms by modulating migration based on turbulent cues.
Over the past decade, the interaction of phytoplankton motility with fluid flow has drawn major attention from both the biology and physics communities. This has led to a deeper understanding of how fluid mechanical cues in the ocean impact the vertical migration of phytoplankton. For example, fluid flow can cause gravitactic cells to form thin layers [3] and microscale patchiness [2]. Recent work indicates that members of two major groups of phytoplankton, raphidophytes and dinoflagellates, display an active, behavioral response to repeated overturning events — imposed through the flipping of an experimental chamber and representative of turbulent cues associated with the smallest turbulent eddies in the ocean [8]. The typical range of values for ocean turbulence lies between \(10^{-9}\) and \(10^{-5}\) \(\textrm{W/kg}\) [5], which corresponds to a Kolmogorov timescale \(\tau K = (\nu \varepsilon)^{1/2}\) in the range \(0.1-30\) \(\textrm{s}\), where \(\varepsilon\) is the energy dissipation rate and \(\nu\) the kinematic viscosity of seawater. Small-scale eddies are experimentally generated by overturnings (flippings) of a millifluidic chamber in the vertical plane over a period of \(18\) \(\textrm{s}\), which corresponds to a turbulent dissipation rate \(\varepsilon = 3 \times 10^{-8}\) \(\textrm{W/kg}\).
Within minutes of experiencing overturning, an upward-swimming population splits into two subpopulations: one that continues to swim upward and one that begins to swim downward. The split is triggered by changes in the cell orientation relative to gravity, as implied by the absence of splitting when flipping occurs in the horizontal plane. This result indicates that the cue for behavioral differentiation is not fluid velocity gradients, but rather changes in the cell orientation relative to gravity, a simple yet fundamental effect of small-scale turbulent eddies that has been previously neglected.
Quantitative morphological analysis of the raphidophyte Heterosigma akashiwo (strain HA452), which forms harmful algal blooms, revealed that a change in cell shape accompanies this behavior; the cells that reversed their swimming direction did so by morphing from an asymmetric “pear shape” to a more symmetric “egg shape.” For an axisymmetric cell of volume \(V\) and density \(\rho_{\textrm{cell}}\) swimming in a fluid of density \(\rho_{\textrm{fluid}}\), the equations for translational and rotational motions are decoupled. This allows one to write force-free conditions along the major- and minor-axes directions as follows:
\[P \sin \phi = D \sin \theta\]
\[P \cos \phi - D \cos \theta = (\rho_{\textrm{cell}} - \rho_{\textrm{fluid}})\: Vg, \tag1 \]
where \(P\) is the propulsion force, acting along the major axis of the cell (\(\phi\) relative to the vertical), and \(D\) is the drag force, acting at an orientation \(\theta\) relative to the vertical. Additionally, balancing the torques around the centre of buoyancy yields
\[D \sin (\theta - \phi) L_H - W \sin \phi L_W = R \eta \omega. \tag2 \]
Figure 2. Regime diagram of cell stability. Colors denote the cell rotation rate ω following an orientational perturbation: ω>0 denotes negatively gravitactic cells (stable upward), ω<0 denotes positively gravitactic cells (stable downward), and ω=0 (white dashed line) denotes neutrally stable cells. Sample asymmetry configurations corresponding to different locations on the regime diagram are illustrated by the black and white schematics. Full circles denote experimental data [8]. The morphological adaptation of HA452 cells in response to overturning causes the population stability to switch (red arrow crossing the white dashed line). The original population splits into a subpopulation swimming downward HA452(↓) and a subpopulation swimming upward, HA452(↑). Adapted from [8].
\(L_H\) and \(L_W\) are the two cellular length scales that correspond to the offset length between \(C_B\) (the geometric center where the buoyancy force acts) and \(C_H\) (the center of hydrodynamic stress where the net hydrodynamic force acts) or \(C_W\) (the center of mass where the weight, \(W\), acts) respectively (see Figure 1). The position of these three points, relevant for cell stability, is obtained using the cell contour, the size and position of the nucleus (determined by epifluorescence microscopy), and the flow field around the cell (obtained via a fluid dynamics model) [8]. The relative position of these points within the cell regulates the strength of the hydrodynamic and gravity torques, determining the cell’s swimming stability and thus ultimately its swimming direction. At a given swimming speed, numerical solution of the system of equations \((1)\) and \((2)\) yields the rotation rate \(\omega(\theta)\) as a function of the swimming orientation to the vertical \(\theta\). The swimming direction \(\theta\) is set by the competition between the gravitational torque \(T_W\) and the hydrodynamic torque \(T_H\) about \(C_B\). Two physical features—summarized by two morphological length scales—determine cell stability: the asymmetry in shape, quantified by \(L_H/a\), and the mass distribution, quantified by \(L_W/a\), where \(a\) is the semi-major axis (see Figure 1). The characteristic reorientation timescale determines cell stability based on the fact that greater stability will cause faster reorientation toward the stable orientation after a cell’s perturbation. In the phase space of cell stability defined by the two cellular length scales \(L_H\) and \(L_W\), the loss of fore-aft asymmetry corresponds with the crossing of the line that divides upward and downward stability regimes (see Figure 2).
These findings illustrate that phytoplankton are capable of precise control over movement behavior through fine-scale control of cellular morphology in rapid response to environmental cues. This discovery paves the way for a new class of mathematical models in which single phytoplankton cells sense turbulent cues and rapidly adapt their motility strategy. By establishing a mechanistic link between turbulence, cell physiology, and emergent behavior, the proposed framework contributes to our understanding of phytoplankton distributions in current and future oceans.
Acknowledgements: This work was co-funded by a Human Frontier Science Program Cross Disciplinary Fellowship (LT000993/2014-C to A.S.), a Swiss National Science Foundation Early Postdoc Mobility Fellowship (to F.C.), and a Gordon and Betty Moore Marine Microbial Initiative Investigator Award (GBMF 3783 to R.S.).
References
[1] Bollens, S.M., Rollwagen-Bollens, G., Quenette, J.A., & Bochdansky, A.B. (2011). Cascading migrations and implications for vertical fluxes in pelagic ecosystems. J. Plankton Res., 33, 349-355.
[2] Durham, W.M., Climent, E., Barry, M., De Lillo, F., Boffetta, G., Cencini, M., & Stocker, R. (2013). Turbulence drives microscale patches of motile phytoplankton. Nat. Commun. 4, 2148.
[3] Durham, W.M., Kessler, J.O., & Stocker, R. (2009). Disruption of vertical motility by shear triggers formation of thin phytoplankton layers. Science, 323, 1067-70.
[4] Karp-Boss, L., Boss, E., & Jumars, P.A. (2000). Motion of dinoflagellates in a simple shear flow. Limnol. & Oceanogr., 45, 1594-1602.
[5] Lozovatsky, I., Lee, J., Fernando, H.J.S., Kang, S.K., & Jinadasa, S.U.P. (2015). Turbulence in the East China Sea: the summertime stratification. J. Geophys. Res. Oceans, 120, 1856-1871.
[6] Margalef, R. (1977). Life-forms of phytoplankton as survival alternatives in an unstable environment. Oceanologia, 1, 493-509.
[7] Schuech, R., & Menden-Deuer, S. (2014). Going ballistic in the plankton: Anisotropic swimming behavior of marine protists. Limnol. Oceanogr. Fluids Environ., 4, 1-16.
[8] Sengupta, A., Carrara, F. & Stocker, R. (2017). Phytoplankton can actively diversify their migration strategy in response to turbulent cues. Nature, 543, 555-558.
[9] Smayda, T.J. (2010). Adaptations and selection of harmful and other dinoflagellate species in upwelling systems. 1. Morphology and adaptive polymorphism. Prog. Oceanogr., 85, 71-91.
[10] Sullivan, J.M., Swift, E., Donaghay, P.L., & Rines, J.E.B. (2003). Small-scale turbulence affects the division rate and morphology of two red-tide dinoflagellates. Harmful Algae, 2, 183-99.
[11] Zirbel, M.J., Veron, F., & Latz, M.I. (2000). The reversible effect of flow on the morphology of Ceratocorys horrida. J. Phycol., 58, 46-58.
Anupam Sengupta is a Human Frontiers Cross Disciplinary Fellow at ETH Zürich. He holds a Ph.D. in physics and works at the interface of fluid mechanics, material sciences, and microbial ecology. Francesco Carrara is a postdoctoral researcher at ETH Zürich. His research interests include spatial and community ecology and biophysics of microorganisms, with applications for aquatic ecosystems. Roman Stocker is a professor of environmental engineering at ETH Zürich. His research focuses on understanding the physical ecology of microbes in aquatic and other environments.