Paleo-structure of the Earth’s Mantle

By Hans-Peter Bunge

Mantle convection is vital to our Earth system. The relentless deformation produced inside the Earth’s mantle by slow, viscous creep has a far greater impact on our planet than might be immediately evident. Continuously reshaping the Earth’s surface, mantle convection provides the enormous driving forces necessary to support large-scale horizontal motion in the form of plate tectonics and the associated earthquake and mountain-building activity. At the same time, mantle convection induces substantial vertical motion in the form of topography dynamically maintained by lateral pressure gradients beneath tectonic plates. This vertical motion, on the order of 1 km or so, is perhaps the most spectacular manifestation of mantle convection—and its most enduring impact upon the entire Earth system. It is expressed ultimately on all scales—local, regional, global—through sea level variations and flooding events known from the geologic record to have reached deep into the interiors of continents (see Figure 1), with profound consequences for the opening and closure of marine pathways and their impact on the global climate system.The link between deep mantle processes and their surface manifestations is an issue of direct practical relevance, in particular concerning the evolution of sedimentary basins and their paramount economic importance in terms of hydrocarbon and other resources (see [4] for a recent review).

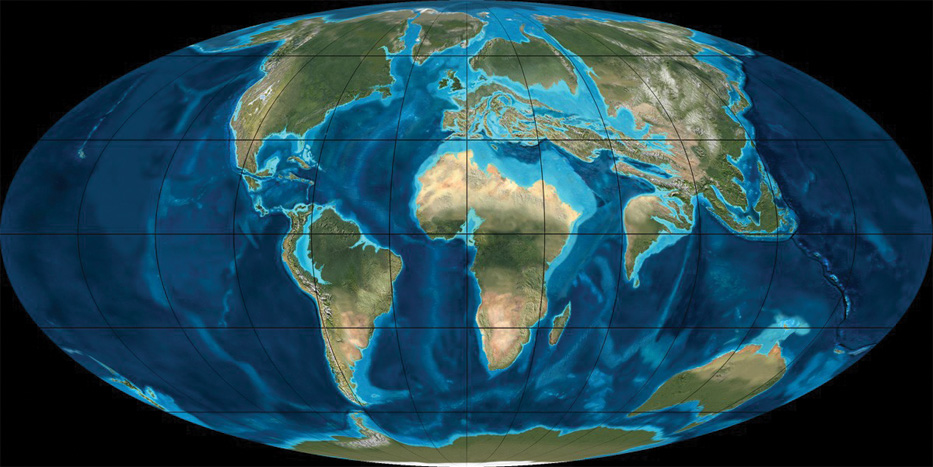
Figure 1. Schematic representation of Earth’s paleogeography corresponding to conditions in the Eocene, some 50 million years ago. In the comparatively recent Eocene epoch (less than 1% of Earth’s history has occurred since), the Earth system differed substantially from today, with extended inland seas covering portions of the continents, e.g., in northern Africa, central Europe, and parts of Russia. In these regions Earth’s mantle experienced substantial change because of active subduction of the ancient Tethys ocean. Subsidence in the Tethys realm had a profound impact on ocean circulation and climate, enabling the formation of equatorial marine pathways that are mostly closed now and serving as a major depositional centre. Whereas the distribution of marginal (inland) seas can be inferred reasonably well from paleo-shorelines, greater uncertainty is associated with the subarial paleotopography depicted here. Image from the paleogeography maps of R. Blakey, Northern Arizona University; www2.nau.edu/rcb7.

The time scale of geologic processes, typically on the order of millions of years, is sufficiently long that the Earth’s mantle, although stronger than steel and capable of transmitting seismic shear waves, can be treated as a fluid. Mantle convection is thus governed by hydrodynamic field equations expressing the fundamental principles of mass, momentum, and energy conservation. Here, the form of the momentum equation is of particular interest. Because of the very high viscosity of the Earth’s mantle (in the range of 10²¹ Pa·s), the momentum conservation law simplifies to the Stokes equation, where the inertia terms can be ignored owing to the negligible flow velocities (on the order of cm/year) and accelerations. The resulting instantaneous balance of frictional and buoyancy forces is represented by an elliptic partial differential equation, with driving forces for the flow arising from lateral density anomalies in the mantle. Time-dependence enters the mantle convection system through the energy equation, which describes the transport of heat inside the Earth’s mantle by advection and conduction.

A rich spectrum of physics is compatible with the governing equations. Powerful computer models are available for simulating the mantle convection process (see [12] for a recent review), and software development now under way opens a path to exascale computing [3,8]. But grave uncertainties compromise our knowledge of crucial material parameters (temperature, composition, strength) in the mantle. In principle, it is possible to resolve these uncertainties by testing mantle convection models against data, such as paleo-shorelines or variations in the structure of sedimentary basins, gleaned from the geologic record. But geologic events—by definition—happened in the past. Modeling paleo-mantle convection currents so that they can be linked explicitly to the geologic record thus requires knowledge of the state of the convective system in the past, which, of course, is not available to us.

Over the past two decades, geophysicists have constructed mantle circulation models (MCMs) to overcome the initial condition problem [1]. Such models (see Figure 2) compensate for the lack of initial condition information by postulating a priori a pattern of mantle heterogeneity for an earlier geologic period. In this approach a given model is integrated forward to the time of interest, with a model for the history of past plate motion (see [10] for a recent review) serving as the surface boundary condition for velocity in the momentum equation. It would be impossible to obtain meaningful MCMs without the geologic record of past plate motion: Tectonic plates cover 80% of the total surface area of the mantle, with the core–mantle boundary (CMB) accounting for the other 20%. Thus, past plate motion models constrain the history of mantle surface velocities by 80%, vastly reducing the non-uniqueness inherent in attempts to model mantle flow through time. MCMs have yielded key insight into the relation of mantle structure and the history of plate motion. In particular, they demonstrated that much of the large-scale structure of Earth’s mantle can be attributed to the sinking of dense, old ocean floor to the CMB, and that the mantle is likely to be of uniform chemical composition at the scale of convection cells [9].

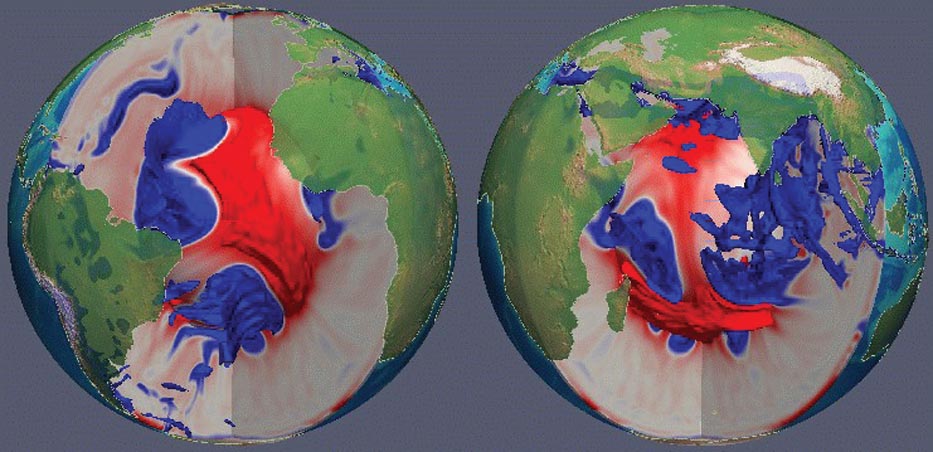
Figure 2. Thermal structure in a mantle circulation model. The adjacent cross sections are centered on 35° (left) and 305° (right) longitude, and the color scale is saturated at –400 K and +400 K. Continents with color-coded topography are superimposed for geographic reference. Isosurfaces of temperature are displayed for –600 K and +400 K, with the +400 K isosurface clipped in the uppermost 500 km to allow views into the mantle underneath the mid-ocean ridge system. The reduced thermal heterogeneity in the upper mantle is a consequence of the low viscosity and high mobility of the flow there. Notice the prominent and hot deep mantle upwellings, in particular beneath the African continent.

The ad hoc nature of the initial conditions assumed in MCMs is a grave limitation and has prompted an alternative approach, known as backward advection. Here, an estimate for present day mantle structure, commonly derived from global-scale seismic imaging, serves as the initial condition for a flow calculation, which is then integrated backward in time, neglecting thermal diffusion; such models give access to the secular variation of the mantle heterogeneity field. Backward advection exploits the immense convective vigour of the mantle—i.e., for short time periods, on the order of a few million years, thermal advection (which is time-reversible) dominates diffusion. Running mantle convection models back in time has given us a glimpse of many of the geologic phenomena affected by secular mantle variations. For instance, we have learned that motion of so-called mantle hotspots, like Hawaii, and changes in the position of Earth’s rotation axis over geologic time are associated with the evolving mantle density structure (e.g., [11]). The primary reason for the failure of backward integration as a viable strategy for inferring mantle paleo-structure is simple: It leads to an accumulation of artifacts, especially near thermal boundary layers, where diffusion is, by definition, important; these are not optimal conditions for retrieving the mantle paleo-state [2].

For this reason, optimisation techniques are now coming to the fore as a powerful approach to the recovery of past deep Earth structure. Geophysicists seek solutions that minimise the difference between mantle heterogeneity inferred (in some form) from seismic imaging and predictions of dynamic models, subject to optimal initial conditions. This is an inverse problem for which time is a variable. Crucial to its solution is that the model derivative be found relative to the unknown initial state. Obtaining the derivative by means of classical finite differencing techniques is, of course, impractical due to the large number of parameters (in the range of 10¹²) in modern dynamic Earth models. The adjoint method, advocated early on in meteorology [13] and seismology [14], is a mathematically elegant and computationally efficient method for obtaining the gradient information needed in the inversion. Rapidly increasing computational resources are making the adjoint approach attractive across the geosciences—in, for example, oceanography [16], seismology [5,6,15], and geo-dynamo simulations [7]. The adjoint equations for mantle dynamics and detailed discussions of model, data, and parameter errors can be found in [2]. Paleo-structure modeling of the Earth’s mantle will provide crucial information on the history of plate-driving forces, the material properties of the deep Earth, and the temporal evolution of the CMB, as well as a deeper understanding of the development of sedimentary basins, thereby advancing us into an era of integrated investigations that will alter our view of the Earth system.

References
[1] H.-P. Bunge et al., Time scales and heterogeneous structure in geodynamic earth models, Science, 280 (1998), 91–95.
[2] H.-P. Bunge, C.R. Hagelberg, and B.J. Travis, Mantle circulation models with variational data assimilation: Inferring past mantle flow and structure from plate motion histories and seismic tomography, Geophys. J. Int., 152 (2003), 280–301.
[3] C. Burstedde et al., Large-scale adaptive mantle convection simulation, Geophys. J. Int., 192 (2013), 889–906.
[4] S. Cloetingh et al., TOPO-EUROPE: The geoscience of coupled deep Earth and surface processes, Global and Planet. Change, 58 (2007), 1–118.
[5] A. Fichtner, H.-P. Bunge, and H. Igel, The adjoint method in seismology, I: Theory, Phys. Earth Planet. Inter., 157 (2006), 86–104.
[6] A. Fichtner, H.-P. Bunge, and H. Igel, The adjoint method in seismology, II: Applications: Traveltimes and sensitivity functionals, Phys. Earth Planet. Inter., 157 (2006), 105–123.
[7] A. Fournier et al., An introduction to data assimilation and predictability in geomagnetism, Space Sci. Rev., 155 (2010), 247–291.
[8] B. Gmeiner, U. Rüde, H. Stengel, C. Waluga, and B. Wohlmuth, Performance and scalability of hierarchical hybrid multigrid solvers for Stokes systems, 2013, submitted, SIAM J. Sci. Comput.
[9] B.S.A. Schuberth, H.-P. Bunge, and J. Ritsema, Tomographic filtering of high-resolution mantle circulation models: Can seismic heterogeneity be explained by temperature alone?, Geochem. Geophys. Geosyst., 10 (2009). 
[10] M. Seton et al., Global continental and ocean basin reconstructions since 200 Ma, Earth Sci. Rev., 113 (2012), 212–270.
[11] B. Steinberger and R.J. O’Connell, Changes of the earth’s rotation axis owing to advection of mantle density heterogeneities, Nature, 387 (1997), 169–173.
[12] P.J. Tackley, Dynamics and evolution of the deep mantle resulting from thermal, chemical, phase, and melting effects, Earth Sci. Rev., 110 (2012), 1–25.
[13] O. Talagrand, Assimilation of observations, an introduction, J. Meteorol. Soc. Japan, 75 (1997), 191–209.
[14] A. Tarantola, Inversion of seismic reflection data in the acoustic approximation, Geophysics, 49 (1984), 1259–1266.
[15] J. Tromp, C. Tape, and Q. Liu, Seismic tomography, adjoint methods, time reversal, and banana-donut kernels, Geophys. J. Int., 160 (2005), 195–216.
[16] C. Wunsch, The Ocean Circulation Inverse Problem, Cambridge University Press, Cambridge, UK, 1996.