By Peter Grindrod, Desmond J. Higham, and Robert S. MacKay
More than half of the world’s population lives in cities, a proportion that is estimated by the World Health Organization to reach 60% by 2030 and 70% by 2050. Thanks to the proliferation of smart devices and interconnected services, cities are gushing data, much of it related to human behavior. City life generates data streams around online social media, telecommunication, geolocation, crime, health, transport, air quality, energy, utilities, weather, CCTV, wi-fi usage, retail footfall, and satellite imaging. The powerful new concept of urban centres as “Living Labs” is inspiring novel research that could lead to improved well-being and economic growth.
We argue here that mathematicians can make an impact at the heart of this emerging interdisciplinary field, where hypotheses about human behavior must be quantified and tested against large-scale data sets, and where decisions and interventions should be based on quantitative, testable predictions. Moreover, the rapid growth of large-scale, disparate, multi-resolution data sets is driving new research challenges for applied and computational mathematicians, drawing on such hot topic areas as dynamic and multiplex networks (see Figures 1 and 2) [4, 9], multiscale modelling and simulation [2], uncertainty quantification [15], and sparse tensors [12, 13].
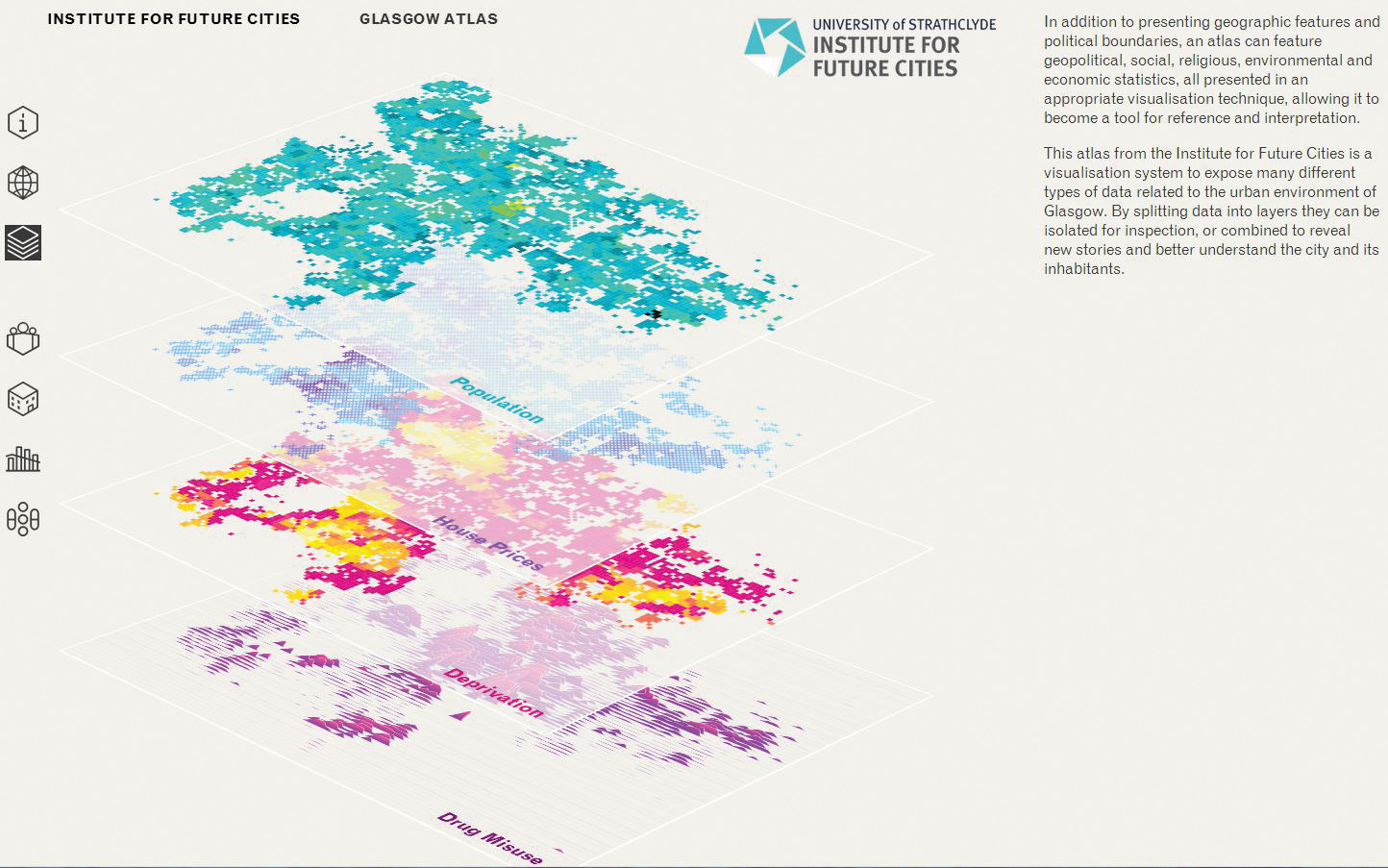
Figure 1. Multiplex visualization of population density, housing cost, deprivation, and drug-use levels across the city of Glasgow, Scotland. © LUSTlab/Institute for Future Cities, University of Strathclyde. Reproduced with permission.
|
The Future Cities research arena we envisage is inherently interdisciplinary, encompassing the physical and social sciences, engineering, business, law, and, in particular, issues of privacy and ethics. At the risk of buzzword overload, we also note extensive overlap with other big-picture themes, including Data Science, Big Data, Complexity, Planet Earth, Digital Economy, the Internet of Things, and Computational Social Science.
Many urban centers around the world are becoming active in the Future Cities space, with strong support for these developments from governments and funding agencies. Focussing just on our home institutions, Glasgow City Council beat out 30 other cities to win a £24 million Future Cities Demonstrator competition, funded by the Technology Strategy Board, the innovation agency of the UK government; under this award, the Institute for Future Cities at the University of Strathclyde is developing a Digital Observatory that will allow public access to data generated in Glasgow and elsewhere. Future Cities is also one of the four strategic themes for Strathclyde’s £89 million Technology and Innovation Centre, a hub for academic research and industrial collaboration. The University of Oxford’s Engineering and Physical Sciences Research Council (EPSRC) Centre for Doctoral Training in New Industrially Focused Mathematical Modelling has a strong data analytics/technology component, and its Said Business School hosts the Institute for New Economic Thinking. The University of Warwick, which has designated Sustainable Cities as one of its Global Research Priorities, houses the Warwick Institute for the Science of Cities and offers an EPSRC Centre for Doctoral Training in Urban Science. The University of Warwick is also a partner in the Center for Urban Science and Progress (CUSP; http://cusp.nyu.edu/about/), a public/private research collaboration that uses New York City as a laboratory and classroom, and in its recently announced branch “CUSP London.”
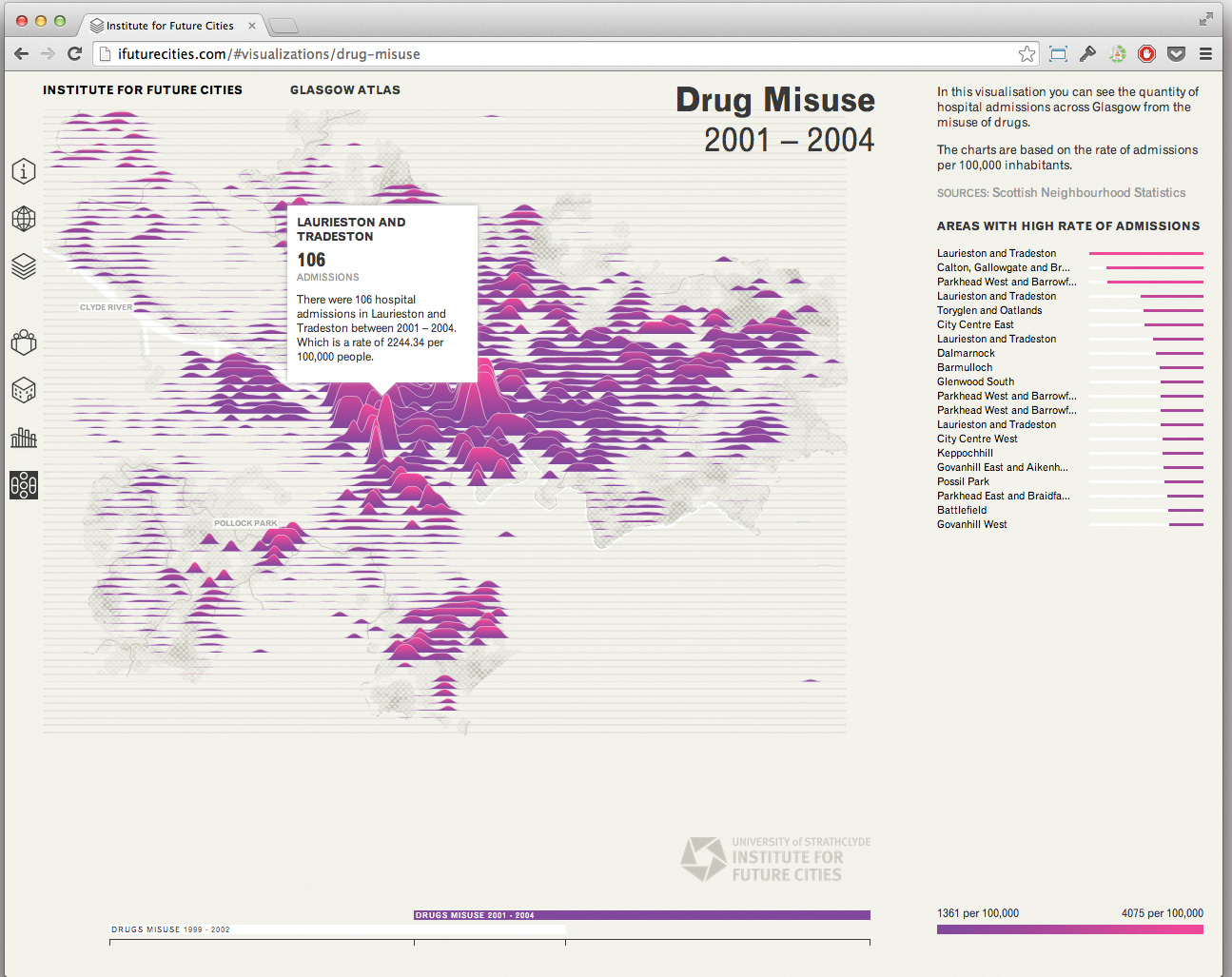
Figure 2. Reported levels of drug use across Glasgow, in a screen shot from the data streams of Figure 1. After discretisation based on, for example, city regions, combination of the levels in Figure 1 leads naturally to a three-dimensional tensor, with two dimensions representing spatial coordinates and the third dimension indexing the data sources. Time dependency in the data would add a fourth dimension. Extracting commonalities and differences, and summarising patterns, can be cast in terms of tensor factorisation––for example, generalising the matrix-level singular value decomposition. These four dimensions are not comparable––any results should be insensitive to the order in which we label the data streams, but for most purposes we should not reorder points in time or space. © LUSTlab/Institute for Future Cities, University of Strathclyde. Reproduced with permission.
|
Further afield, Horizon 2020, the biggest European Union research and innovation programme to date, chose Societal Challenges as one of its three pillars, listing a €100 million call for research projects under the theme Smart Cities and Communities. In a draft strategic plan released in July 2014, EPSRC identified “designing and building future cities” as one of seven key challenges for the global economy.
A report commissioned by the UK Department for Business, Innovation and Skills [11] considered opportunities for UK industry in smart city technology across five urban market sectors––energy, water, transport, waste, and assisted living––estimating a global market of $408 billion by 2020.
Future Cities and the Math Sciences
We conclude with a brief look at recent developments and prospects in dynamical systems and in networks, with the focus mainly on our own research interests.
Macroscale observations have revealed scaling laws that relate city population size to such attributes as energy consumption, household income, and patent production, and important distinctions have been drawn between linear, sublinear, and superlinear growth [1, 14]. Explanatory, microscale models based on “hidden” laws must be consistent with such observations. Long-time dynamics and stability are key issues in the modelling of complex urban systems, as are sensitivities to parameter choices, including thresholds imposed by resource limitations [5]. In principle, good mathematical models can be used to map out ranges of possible behavior: An observed phenomenon might be constrained within a single domain of attraction (with others as yet unseen) and have a very low probability of breaking out; alternatively, it might reflect the trajectory of a chaotic process, where the qualitative macroscopic behaviour is predictable but the quantitative evolution of specific individuals is not (because of sensitive dependence on initial conditions and instability-driven disruptions).
In modelling terms, surgical extraction of the city from its surroundings may not be appropriate, and an open model, subject to a range of external influences, may be more realistic. Phenomena of interest might then be subject to persistent cycling or boiling, without ever approaching quiescence [17].
Digital interactions in an urban setting can naturally be represented as graphs, or networks, but the links between nodes in the system typically have an important time-dependent feature: Who just texted whom, who just logged on to which free wi-fi zone, who just reported a crime at which location? In a previous article in SIAM News, two of us discussed how a dynamic view of classical concepts in graph theory led to useful new algorithms [8]. But alongside the data-driven issue of extracting and summarizing information from network observations is the equally compelling challenge of deriving models that describe the underlying dynamics. Representing a network as a time-dependent matrix \(A(t)\) whose \((i, j)\) element quantifies the current level of interaction between nodes \(i\) and \(j\), we can formalize concepts from the social sciences to derive suitable laws of motion (see sidebar).
In an urban context, where dynamic interactions take place on many levels between a range of parties, it is natural to think of dynamic models that operate across many layers, with the dynamics on one layer (e.g., the evolution of attitudes toward healthy lifestyle) coupled to the dynamics on another (e.g., the reach of a social media campaign). Moreover, with the advent of smartphones and GPS, we can now monitor geographic location across time and hence test models of urban movement [10].
In the preamble to his recent book The New Science of Cities [3], Michael Batty of the Bartlett Centre for Advanced Spatial Analysis at University College London discusses three central principles that inform his “networks and flows” perspective of city science; all three resonate strongly with the standpoint of this article. Batty’s first principle is that the relations between objects, not the intrinsic attributes of those objects, should condition our understanding, a viewpoint familiar to those who have been exposed to graph theory or category theory. Second, we should aim to measure, categorize, and look for universal scalings when we observe and compare city networks across space and time. Third, having gathered macro-level observations, we should seek to understand the micro-level principles that drive them––or, in the language of applied mathematics, we should aim for explanatory models, based on explicit modelling assumptions, with predictive power. Batty’s book makes use of such concepts as agent-based modelling, flocking, graph theory, Markov chains, Markovian decision problems, optimization, and self-similarity/fractals, and hence is an excellent starting point for mathematicians wishing to enter the field.
In the spirit of micro-level digital interactions, one of us has initiated a LinkedIn group on MSSC: Mathematical Sciences for Smart Cities. Interested readers are encouraged to join us.
Acknowledgments: The authors are supported by the Engineering and Physical Sciences Research Council (Mathematical Sciences), the Research Council UK Digital Economy programme, and the Royal Society/Wolfson Foundation.
References
[1] E. Arcaute, E. Hatna, P. Ferguson, H. Youn, A. Johansson, and M. Batty, City boundaries and the universality of scaling laws, Tech. Rep., arXiv:1301.1674, January 2013.
[2] M. Batty, Agents, cells, and cities: New representational models for simulating multiscale urban dynamics, Environ. Planning A, 37 (2005), 1373–1394.
[3] M. Batty, The New Science of Cities, The MIT Press, Cambridge, MA, 2013.
[4] S. Boccaletti, G. Bianconi, R. Criado, C.I.D. Genio, J. Gómez-Gardeñes, M. Romance, I. Sendiña-Nadal, Z. Wang, and M. Zanin, The structure and dynamics of multilayer networks, Phys. Rep., (2014), to appear.
[5] V.I. Dmitriev, E.S. Kurkina, and O.E. Simakova, Mathematical models of urban growth, Comput. Math. Model., 22 (2011), 54–68.
[6] P. Grindrod and D.J. Higham, A dynamical systems view of network centrality, Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci., 470 (2014), to appear.
[7] P. Grindrod, D.J. Higham, and M.C. Parsons, Bistability through triadic closure, Internet Math., 8 (2012), 402–423.
[8] D.J. Higham, P. Grindrod, and E. Estrada, People who read this article also read . . . :Part I, SIAM News, 44:1 (2011), 1–3; Part II, 44:2 (2011), 2–3.
[9] M. Kivelä, A. Arenas, M. Barthelemy, J.P. Gleeson, Y. Moreno, and M.A. Porter, Multilayer networks, J. Complex Networks, (2014), to appear.
[10] A. Noulas, S. Scellato, R. Lambiotte, M. Pontil, and C. Mascolo, A tale of many cities: Universal patterns in human urban mobility, PLoS ONE, 7 (2012), e37027.
[11] Ove Arup & Partners Limited, The Smart City Market: Opportunities for the UK, Department of Business Innovation and Skills, UK Government, Research paper 136, 2013.
[12] E.E. Papalexakis, T.M. Mitchell, N.D. Sidiropoulos, C. Faloutsos, P.P. Talukdar, and B. Murphy, Scoup-SMT: Scalable coupled sparse matrix-tensor factorization, arXiv:1302.7043, 2013.
[13] M.D. Schatz, T.-M. Low, R.A. van de Geijn, and T.G. Kolda, Exploiting symmetry in tensors for high performance, SIAM J. Sci. Comput., to appear.
[14] M. Schläpfer, L.M.A. Bettencourt, S. Grauwin, M. Raschke, R. Claxton, Z. Smoreda, G.B. West, and C. Ratti, The scaling of human interactions with city size, J. R. Soc. Interface, 11 (2014), 20130789.
[15] R.C. Smith, Uncertainty Quantification: Theory, Implementation, and Applications, SIAM, Philadelphia, 2014.
[16] V.A. Traag, P. Van Dooren, and P. De Leenheer, Dynamical models explaining social balance and evolution of cooperation, PLoS ONE, 8 (2013), e60063.
[17] J. Ward and P. Grindrod, Aperiodic dynamics in a deterministic model of attitude formation in social groups, Tech. Rep., arXiv:1302.0164, 2013.
Peter Grindrod is a professor at the Mathematical Institute of the University of Oxford. Desmond J. Higham is a professor in the Department of Mathematics and Statistics at the University of Strathclyde. Robert S. MacKay is a professor in the Mathematics Institute and Centre for Complexity Science at the University of Warwick, UK.
Social Balance
Traag, Van Dooren, and De Leenheer [16] looked at the concept of social balance (my friend’s friend is my friend, my enemy’s enemy is my friend, . . .) to derive matrix-valued ordinary differential equations of the form \(\dot{A}(t) = A(t) \times A(t)\) and \(\dot{A}(t) = A(t) \times A(t)^T\). Given such an \(A(t)\), two of us [6] developed an accompanying ODE for the level of importance, or centrality, of the network nodes, showing that the matrix logarithm function arises naturally.
An alternative concept from the social sciences, triadic closure (the more friends I have in common with a person, the more likely I am to become the person’s friend), was used in [7] to derive a stochastic birth and death model for link dynamics. There, results of mean-field analysis agreed with simulations showing that the network can self-organize into either of two very different long-term behaviors.