By Oliver E. Jensen
Until a few years ago I knew very little about plants, despite the fact that––as harvesters of solar energy, atmospheric regulators, and a primary food source––they underpin our existence on this planet. My turning point came in 2007, when I had the good fortune to join a systems biology project at the University of Nottingham, UK, created to develop a “virtual root.” This opened my eyes to the remarkable ways in which even the most humdrum weed is able to exploit and adapt to its environment. The project also turned out to be an excellent testbed for the development of multiscale mathematical models connecting mechanics to biology.
Plant growth is tempered by numerous signals. Underground, a root can respond to gravity, water gradients, distribution of nutrients such as phosphate and nitrate, and soil stiffness. The hope for the virtual root project is that an understanding of how a plant senses, integrates, and responds to these competing signals will contribute to the development of improved crop species that can thrive in challenging climatic conditions and harsh agricultural environments.
Mathematicians, engineers, and computer scientists have an important role to play in this endeavour. Quantitative descriptions of growth and biological development are essential if we are to get to grips with the full complexity of living organisms. At the same time, to avoid problems of computational intractability, we need efficient techniques to handle interactions spanning widely disparate space- and time-scales. And alongside the traditional components of systems biology––intricate networks describing interactions between genes and proteins within individual cells––it is essential to account for the spatial organisation of multiple cells in a tissue. This requires consideration of the transport of signals between cells, and of the physical forces that provide mechanical integrity to an organ and ultimately drive its growth.
A natural focus for our project was the species Arabidopsis thaliana, a type of cress that––like the fruit fly in animal biology––is intensively studied because it grows easily and reproduces quickly. Its primary root provides a beautifully organised system for study (Figure 1, left). Stem cells near the root tip divide and differentiate into a small number of cell types, which form tightly adherent concentric layers. Each cell draws in water by osmosis; a stiff cell wall resists inflation, allowing the cell’s internal turgor pressure to rise to a level comparable to that of a car tyre. The cell grows by softening the cell wall, allowing turgor-driven expansion. To stop a cell from inflating like a party balloon, arrays of stiff cellulose fibres embedded in the cell wall ensure that growth is anisotropic: Fibres, wrapped like hoops around a barrel, inhibit radial expansion of a cylindrical cell but allow axial elongation. In this way, a primary root, formed of aligned cylindrical cells (or osmotic micropumps), can expand rapidly along its length in an essentially one-dimensional manner.
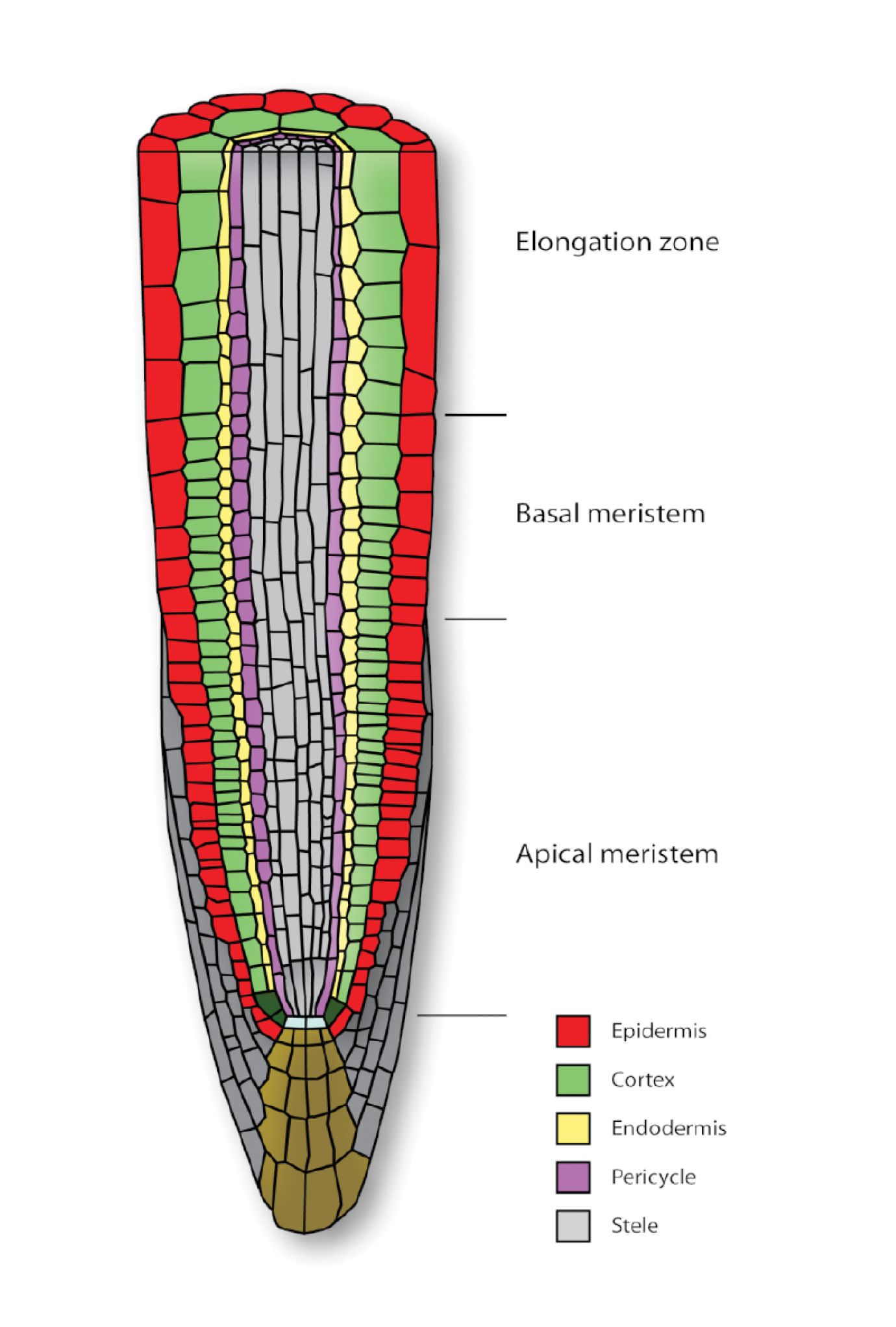 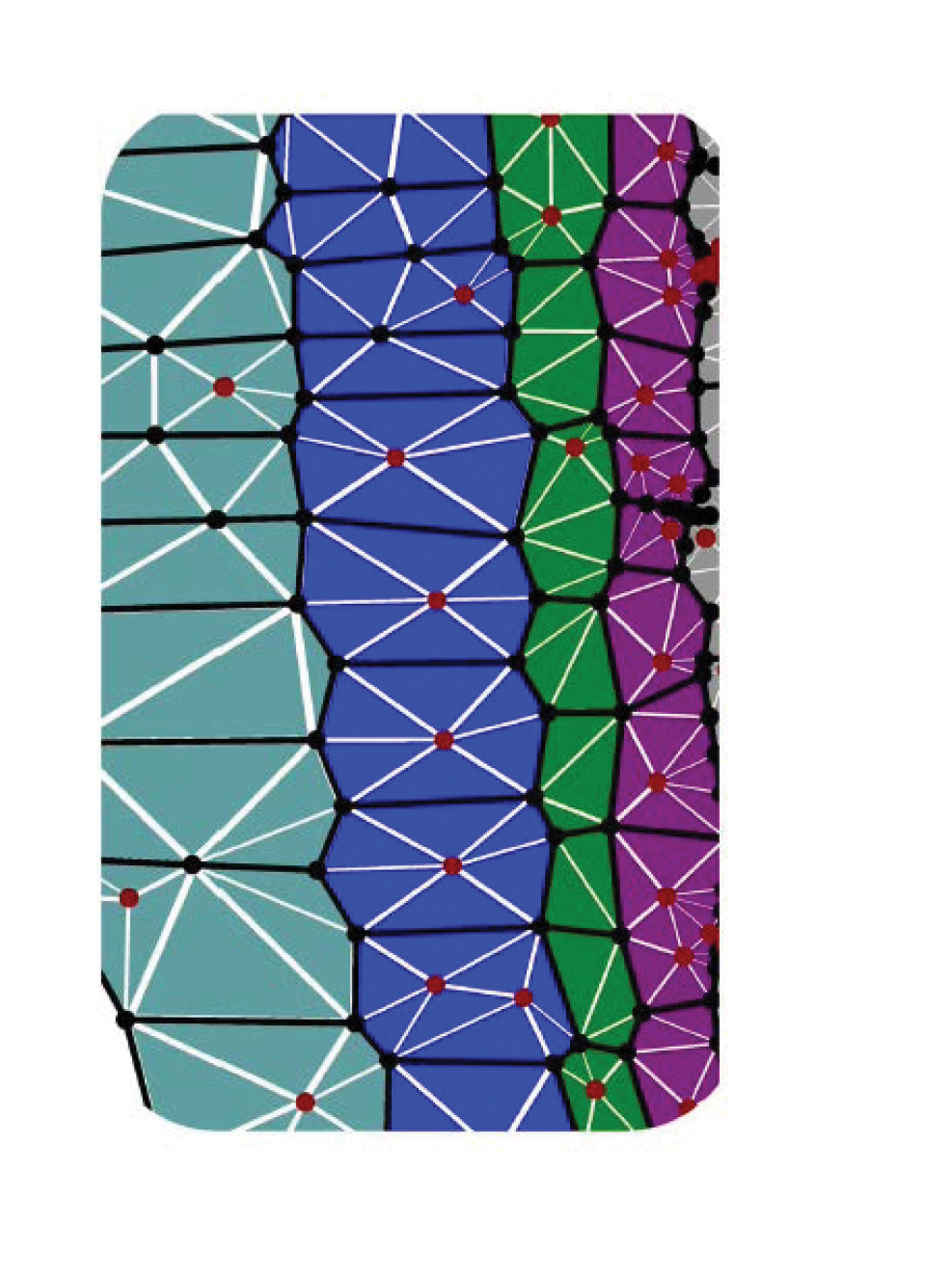
Figure 1. Left. Schematic of the different cell types in the primary root of Arabidopsis. In the frame of reference of the growing root tip, there is an upward flux of cells, driven by cell division in the apical meristem and by cell expansion in the elongation zone. The spatial organisation of cells along the root axis also reveals the cells’ life-histories, with short young cells near the root tip and longer older cells further behind. Gravity-sensing cells are among the brown cells at the root tip. Reprinted from Trends in Plant Science, 14/7, Benjamin Péret et al., Arabidopsis lateral root development: An emerging story, 399–408, 2009, with permission from Elsevier. Right. In computational simulations of cell expansion, individual cells are represented as polygons (in a two-dimensional projection), and mechanical properties are ascribed to the cell walls; walls in the plane of the simulation are divided into elements that account for the reorientation of embedded cellulose microfibrils (from Fozard et al., 2013). Use of realistic cell geometries is important for accurate simulation of the transport of regulators like auxin. |
To model growth, we addressed processes occurring at four distinct spatial levels: an individual cell wall, a single cell, multiple cells in a single cross-section of a root, and multiple cross-sections along the whole axis of the root. Motivated by a simple model dating back to the mid-1960s, we found that a growing cell or tissue can be well described in mechanical terms as viscoplastic: Provided that a yield criterion is satisfied, growth can be modelled as an irreversible stretching deformation that proceeds at a rate characterised by a set of “extensibility” parameters. We adopted a variety of multiscale modelling techniques to derive yield and extensibility parameters appropriate to the different scales. Naturally, geometric factors play an increasingly important role (alongside mechanical properties) as the spatial scales increase.
Our model predicted, for example, that the outermost cell layer in a cylindrical root (the epidermis) has a predominant influence in regulating stretching and bending rates. It is therefore no surprise that the mobile hormone auxin, a key growth regulator, preferentially targets epidermal cells. Auxin also plays a central role in gravitropism, the bending response of a growing root that reorients its tip in the direction of the gravity vector. The mechanism has been known since the 1920s: Gravity-sensing cells in the root tip bias the transport of auxin preferentially toward the underside of the root, promoting a reduction in the cell expansion rate, thereby inducing a bend. Our computational simulation of a gravitropic bend, which represents individual cells as polygons (in a 2D projection), allows the coupling of transport between individual cells and mechanical models that resolve individual cell walls (see Figure 1, right, and www.simuplant.org).
The UK funding councils that supported our project showed considerable vision in allowing the formation of a new multidisciplinary team, giving it time to gel, and allowing an ambitious research programme to develop and mature. Importantly, the mathematical component of the programme was given the space to develop new modelling frameworks that extend beyond Arabidopsis, as well as the opportunity to develop models in tandem with experiments. And, of course, I now have an enduring fascination for plants, weeds included.
References
[1] R.J. Dyson, L. Band, and O.E. Jensen, A model of crosslink kinetics in the expanding plant cell wall: Yield stress and enzyme action, J. Theoret. Biol., 307 (2012), 125-136.
[2] R.J. Dyson and O.E. Jensen, A fibre-reinforced fluid model of anisotropic plant root cell growth, J. Fluid Mech., 655 (2010), 472-503.
[3] R.J. Dyson, G. Vizcay-Barrena, L.R. Band, et al., Mechanical modelling quantifies the functional importance of outer tissue layers during root elongation and bending, New Phytologist, 202 (2014), 1212-1222.
[4] J.A. Fozard, M. Lucas, J.R. King, and O.E. Jensen, Vertex-element models for anisotropic growth of elongated plant organs, Front. Plant Sci., 4 (2013), 233.
Oliver E. Jensen is the Sir Horace Lamb Professor in the School of Mathematics at the University of Manchester.