Mathematical Challenges and Opportunities in Optics and Photonics

By Gang Bao and Michael I. Weinstein

The field of optics and photonics encompasses the fundamental science of light and its applications. The long history of the field’s interactions with mathematics covers topics ranging from ray optics to the classic theory of the electromagnetic spectrum to the quantum nature of light (quantum optics, light–matter interactions). A multitude of technologies that are central to our lives have emerged from these interactions.

The past several decades have witnessed major advances in applications, both realized and potential, that take advantage of the novel properties of light propagation and interactions in complex structures. Examples include super-resolution, optical resonances, near-field imaging, Raman scattering, nonlinear optics, imaging, cloaking, and nano–optics and photonics. These have been brought about by parallel advances in such areas as material fabrication at the micro- and nanoscales, scientific computation (from hardware to algorithms), and a deepening of our understanding of the “multiphysics” of such systems.

This article outlines some of the challenges and opportunities for the applied and computational mathematics community, and discusses recent Optics and Photonics initiatives of the National Science Foundation and the upcoming (2016–17) program in Mathematics and Optics at the Institute for Mathematics and its Applications.

Challenges and Opportunities

As they increase the range of potential applications of optics and photonics, the recent advances present great opportunities and challenges for the applied and computational mathematics community. New modeling tools and techniques are needed, as are new theoretical studies of the underlying PDE-based models and dynamical systems. In addition, novel computational methods must be developed to handle more sophisticated multiscale and multiphysics models.

Optical interactions with nanoscale structures and materials are a prototypical example. To characterize the quantum effects of the interactions, the Schrödinger equation needs to be incorporated into the model; the Maxwell equations alone are no longer adequate. At the same time, because of the computational complexity of the many-body Schrödinger equation, computational techniques must be devised to render such physical processes across many spatial and temporal scales computationally tractable.

We offer the following sample of scientific problem areas in which applied and computational mathematicians have a central role to play, whether by expanding their “toolbox,” by tackling novel applications, or by developing new theory and methods.

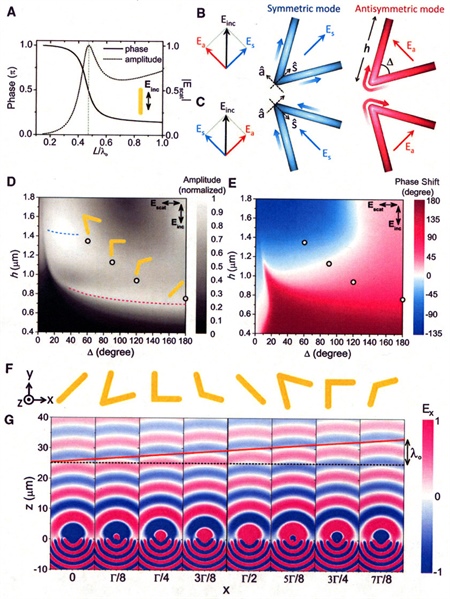
(A) Calculated phase and amplitude of scattered light from a straight rod antenna made of a perfect electric conductor. (B) A V-antenna supports symmetric and antisymmetric modes, which are excited, respectively, by components of the incident field along ŝ and â axes. (C) V-antennas corresponding to mirror images of those in (B). (D and E) Analytically calculated amplitude and phase shift of the scattered light from the V-antennas. (F) V-antenna array that introduces a constant phase gradient along the array. Optical “metasurfaces” constructed by tiling a surface using the antenna array allow demonstration of the generalized laws of reflection and refraction (i.e., arbitrary bending of light beams as they reflect from or pass through the metasurface). (G) Full-wave simulations of the scattered electric field for the individual antennas composing the array in (F), showing that a wave that impinges on the array in the normal direction is deflected into a new direction. From N. Yu et al., Light propagation with phase discontinuities: Generalized laws of reflection and refraction, Science, 334:6054 (2011), doi: 10.1126/science.1210713. Reprinted with permission from AAAS.

Nonlinear optics. Driven by advances in materials science and nano-fabrication, there is intense interest and activity in optical and electromagnetic wave propagation through nonlinear and inhomogeneous media. Nonlinear waves are known to self-focus and/or filament as a result of, for example, the nonlinear optical Kerr effect, in which the local refractive index depends on the light intensity. Optical shocks may occur due to resonances in pulse propagation that are spectrally supported near the zero dispersion point. Can we devise media that suppress, inhibit, or control such singularity formation? What are the novel coherent structures that result from the combination of nonlinearity and microstructure?

Spatial discreteness plays an important role in many linear and nonlinear optical systems; examples include coupled waveguide arrays or lattices, and tight binding in the limits of continuum problems. These models are important to our understanding of energy transport properties for device design and optimization. A new generation of materials and media with novel microstructures are making nonlinear effects accessible to study at lower intensities. The potential for the development of new technologies is huge. Finally, a foundational question concerns the effect of randomness of nonlinear wave propagation—for example, how does the Anderson localization paradigm change in the presence of nonlinearity?

Optimal design, inverse and control problems. Mathematical optimization has long been a fundamental tool for the design of optical systems. Traditionally, ray tracing and asymptotic diffraction models have provided the basis for optimization and design. More recently, as optics and photonics research has focused on phenomena at smaller and smaller length scales, full PDE models have become necessary to adequately capture system behavior. In this realm, device behavior is less intuitive and computational simulations become indispensable. Modern optimal design and optimal control techniques can yield novel designs faster and more efficiently than direct experimentation. Methods of optimization, control, and inverse problems are directed at an extremely diverse range of optical applications, from astronomy to nanoscale optical materials and nanostructures. 

Near-field thermal radiation. Near-field thermal radiation plays a significant role in a variety of emerging applications, including energy conversion, imaging, and precision heating and cooling. The theory for near-field thermal radiation is well described within the framework of fluctuational electrodynamics, which was established half a century ago. Only recently, however, has computational implementation of fluctuational electrodynamics become possible for nonplanar geometries. Meanwhile, the rapid development of nanophotonic and metamaterials has introduced a number of new concepts to the area of near-field thermal transfer.

Nano–optics and photonics. Nano-optics refers to the study of optical phenomena at length scales larger than atomic or molecular, yet smaller than a micron. Exciting opportunities arise from interactions of light and matter at such length scales for the development of nanoscale devices with applications to electronics, optoelectronics, biology, and medicine. The goal is to address systems in which different electromagnetic entities interact—e.g., waveguide modes with surface charges, photons with excitons, plasmons with plane waves. Possible applications include single-molecule spectroscopy, novel microlasers and optical switches, plasmonic materials, optical nanocircuits, Raman scattering, and novel nonlinear photodetectors.

The proper theoretical and computational description of the interaction of optical fields with nanostructures presents significant challenges because of coupled effects over a vast range of scales, giving rise to phenomena not encountered in conventional optics. Important directions include scattering problems for highly localized wavefields, and the roles of plasmonic materials, nonlinearity, anomalous diffraction, and dissipation in photonic phenomena. 

Multiscale problems in optics and electromagnetics. Micro- and nano-structured optical media have huge potential for application to communication and computational devices. Through variations in the materials and their microstructure, it is possible to manipulate a variety of optical properties: dispersion, nonlinear optical effects, resonances through material composition, material contrast, defect geometry, and defect distribution. Common to these problems is the interaction of fields at different spatial and frequency scales in the propagation of light. Novel geometries, broadband frequency ranges, and physically realistic dispersion relations pose important questions for fundamental and applied mathematics.

Classical homogenization theory yields effective properties for the regime of wavelengths much larger than the scale of spatial variations in the microfeatures of the material; the theory of geometric optics/semi-classical analysis, by contrast, is valid in the regime of very short wavelengths, on the scale of the medium’s spatial variations. Many optical and electromagnetic media with novel optical properties fall in the regime in which scales interact. Furthermore, these optical properties are not necessarily valid for a wide frequency spectrum. Central research themes are the relation between time domain equations (which have all frequencies) and the equations that govern single-frequency waves (the Helmholtz and Maxwell equations), and bridging the considerable gap between classical homogenization theory and geometric optics. 

Integration of optics in communications and computation. Many performance-limiting issues in communication networks are related to optical–electrical interfaces. An important technological goal is to develop approaches that seamlessly integrate the two, for example, using recent innovations in silicon nanophotonics. All-optical interconnects will play a central role. Model-based control and simulation techniques need to be developed to optimize the performance.

Initiatives in Optics and Photonics

Several initiatives of the National Science Foundation, now under way, provide a range of opportunities for the mathematical sciences community. Most recently, NSF announced a broad new Optics and Photonics initiative that crosses three directorates: Mathematical and Physical Sciences (with the Division of Mathematical Sciences taking the lead); Engineering; and Computer and Information Science and Engineering [5, 6]. NSF will release a program solicitation in fiscal year 2016.

IMA Annual Program on Mathematics and Optics. During the 2016–17 academic year, the Institute for Mathematics and its Applications at the University of Minnesota will hold the year-long thematic Program in Mathematics and Optics [1]. The program will address the very wide range of questions that arise in the study of optical phenomena and the relevant areas of applied and computational mathematics. The goal is to connect mathematical and computational scientists working on deep problems of optics and photonics with the dynamic interdisciplinary community in the field. The program will also seek to prepare the next generation of applied and computational mathematicians for collaborations with fundamental and applied scientists and engineers.

The IMA Program in Mathematics and Optics will be built around multiple week-long tutorials and workshops, and will have a visitors program. Broad areas slated for coverage include the interaction of light with novel photonic micro- and nano-structures and resonant metamaterials, optimal design and control, and  nonlinear phenomena. An overarching theme of the workshops is the role of classical and developing ideas in multiscale analysis and computation in optics and photonics. 

Among the topics of proposed workshops are:

• Control of waves in resonant materials
• Optimal design and control in optics and photonics 
• Nonlinear optics and photonics
• Multiscale problems in micro- and nano-structures 
• Photonic band-gap structures and  “topological photonics”
• Near-field thermal radiation
• Multiscale computational methods in optics and photonics
• Imaging and sensing

Conclusion

The search for an understanding of optical phenomena and strategies for their control has been a catalyst of pure and applied mathematics in many areas: dynamical systems, ordinary and partial differential equations, harmonic analysis, calculus of variations, geometry, and functional analysis. Conversely, developments in the mathematical and computational sciences have provided foundational tools for the discovery of new phenomena, and for the development of deeper physical theories and their application.

Optical phenomena span vast temporal and spatial scales: macro­scales, governed by Maxwell’s equations with macroscopic constitutive relations; intermediate (mesoscopic) wavelength-scales, e.g., where wavelength and micro-feature dimensions are of the same order; and nano- and atomistic scales, requiring quantum descriptions governed by the Schrödinger equation. Different mathematical concepts and techniques have long played a role in the analysis of each of these regimes—for example, homogenization at the macroscale, coupled-mode theory at the mesoscale (e.g., Bragg resonance), semi-classical analysis in the quantum regime. Many challenges, applied and fundamental, arise from the coupling of these regimes, and modern applied and computational mathematics has a very important role to play.

References
[1] IMA 2016–2017 Annual Program on Mathematics and Optics, Minneapolis, MN; http://www.ima.umn.edu/programs/annual/.
[2] National Research Council, Harnessing Light: Optical Science and Engineering for the 21st Century, National Academy Press, Washington, DC, 1998; http://www.nap.edu/catalog/
5954/harnessing-light-optical-science-
and-engineering-for-the-21st-century.
[3] National Research Council, Optics and Photonics: Essential Technologies  for  Our  Nation, National Academy Press, Washington, DC, 2012; http://www.nap.edu/catalog/
13491/optics-and-photonics-essential-
technologies-for-our-nation.
[4] National Research Council, Photonics: Maintaining Competitiveness in the Information Era, National Academy Press, Washington, DC, 1988; http://www.nap.edu/catalog/1145/
photonics-maintaining-competitiveness
-in-the-information-era.
[5] National Science Foundation, NSF Dear Colleague Letter—Optics and Photonics, NSF 14-091, 2014; http://www.nsf.gov/pubs/2014/nsf14091/nsf14091.jsp.
[6] Science Opportunities in Optics and Photonics, Report of the Optics and Photonics Subcommittee of the MPS Advisory Committee, National Science Foundation, 2014; http://nsf.gov/mps/advisory/mpsac_other_reports/optics_and_photonics-final_from_subcommittee.
pdf. 

Gang Bao ([email protected]) is a professor of mathematics at Zhejiang University. Michael I. Weinstein ([email protected]) is a professor of applied mathematics and of mathematics at Columbia University.