By Lorena A. Barba and Rio Yokota
“Complexity trumps hardware,” according to the conventional wisdom. It is natural that as computers get faster, people want to solve larger problems, eventually bringing fast algorithms to the forefront. This thought was likely in SIAM past-president Nick Trefethen’s mind when, in his 1998 “Predictions for Scientific Computing, Fifty Years from Now,” he declared that fast multipole methods would be ubiquitous. With the irreversible move toward parallel computing of the last decade, however, much of the conventional wisdom began to expire. How, we wonder, will FMM fare in the exascale era?
The non-stop trend in computer architectures today sees the breadth of parallelism increasing rapidly, while memory bandwidth grows much more slowly than processing speed. Overall byte-to-flop ratios (machine balance) are declining—relentlessly—at every level of memory. For now, algorithm designers must respond by striving to reduce data movement and synchronization points, even at the cost of more arithmetic operations. But in some cases, the only way forward may be either a change in the numerical engine or a complete mathematical reformulation of the problem. Such is the pressure from evolving computer architectures that algorithms with large communication and synchronization requirements could become obsolete.
Machine balance is converging: Almost all current architectures saturate at between 0.2 and 0.285 byte/flop (the exception, Fujitsu, at 0.36 byte/flop, is very expensive hardware). Unfortunately, a conflict exists between algorithmic complexity and arithmetic intensity (measured in flop/byte, the inverse unit of machine balance). Thus, algorithms with \(\mathcal{O}(N^2)\) complexity, such as direct \(N\)-body or molecular dynamics, have high flop/byte ratios and high levels of parallelism. Conversely, the ideal \(\mathcal{O}(N)\) algorithms require few operations per data point and tend to have more dependencies, e.g., the stencil operations of finite-difference or finite-element methods. FMM distinguishes itself by offering \(\mathcal{O}(N)\) complexity as well as high flop/byte ratios. In Figure 1, which shows a roofline model of several current architectures along with the arithmetic intensity of representative algorithms, FMM computations tend to lie well under the flat part of the roof. This may explain why the computational science community is more and more interested in FMM and related methods.
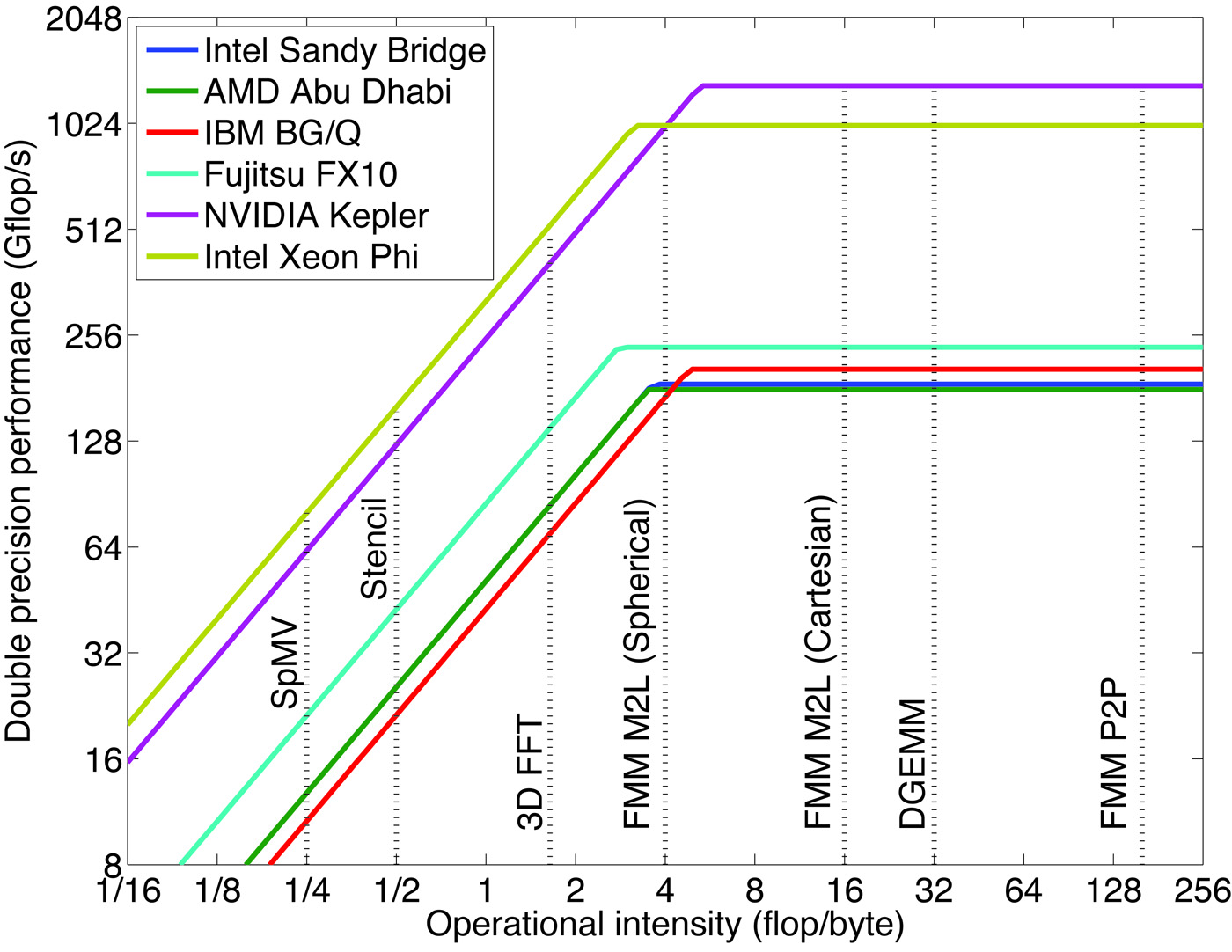
Figure 1. Roofline model of current microarchitectures and operational intensity of representative algorithms. SpMV is a sparse matrix–vector multiplication, Stencil is a multigrid method with a seven-point finite-difference stencil, 3D FFT is a three-dimensional fast Fourier transform, and DGEMM is a dense matrix–matrix multiplication. FMM M2L (spherical) and FMM M2L (Cartesian) are FMM kernels corresponding to interactions between distant clusters that use, respectively, spherical and Cartesian expansions; FMM P2P is an FMM kernel corresponding to interactions between nearby particles.
|
At the 2013 SIAM Conference on Computational Science and Engineering, topics related to FMM were the focus of at least four minisymposia, a set of 32 talks (MS 11, 31, 72, and 132 in the program). Participants included Leslie Greengard and Vladimir Rokhlin, the creators of FMM, as well as many of their past students and descendants. The sessions covered the latest mathematical developments—e.g., high-order quadrature and well-conditioned formulations for non-smooth geometries—as well as novel applications, including magnetic resonance imaging and algebraic preconditioning. Calculations of acoustic [2], electromagnetic [3], and electrostatic [10] fields continue to be the major application areas for multipole methods. Ongoing efforts are also under way to construct more general fast direct solvers, from both geometric [5] and algebraic [4] points of view. We organized a session that emphasized not only applications of FMM, but also the computer science aspects of autotuning, optimization for GPU hardware, and task-based approaches to parallelism.
In a recent paper we discussed the features of FMM that we believe make it a favorable algorithm for future architectures [8]. In brief, its use of a tree data structure extracts spatial data locality from nonuniform and multiscale resolutions and results in benign synchronization requirements. What’s more, the various FMM kernels are either purely local or present a hierarchical communication pattern. These features have allowed several groups to achieve highly efficient massively parallel computations, using hundreds of thousands of CPU cores [6,7] or thousands of GPUs [9]. Our own results suggest that applications that use an FFT-based numerical engine are at a clear disadvantage compared with FMM in terms of parallel scalability beyond several thousand processes (see Figure 2).
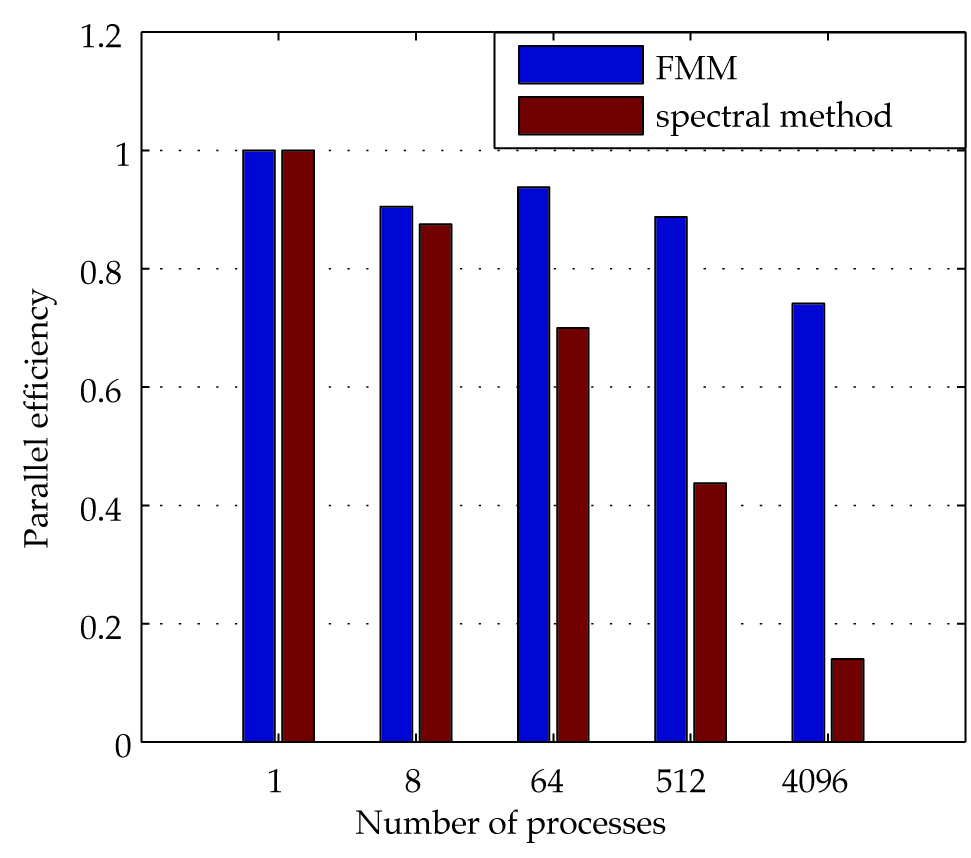
Figure 2. Weak scaling from 1 to 4096 processes of two parallel application codes for fluid turbulence, one using an FMM-based solver on GPUs (one GPU per MPI process), the other an FFT-based solver on CPUs. Figure used under CC-BY license; doi:10.6084/m9.figshare.92425.
|
Some of our colleagues have conveyed a more gloomy outlook, even for FMM [1]. Projecting current architectural trends and offering a new analysis of communication that is calibrated to the state-of-the-art implementation of the kernel-independent version of FMM (known as k i fmm), they predicted that FMM will become memory-bound by 2020. Re-inspection of Figure 1 shows that with our FMM code (called exaFMM), we obtain an arithmetic intensity of 4 flop/byte on the box–box interactions (far-field) using spherical expansions. This lies on the edge of the compute-bound “flat roof.” If machine balance worsens as peak performance increases and the inclined part of the roofline extends to the right, this kernel can indeed become bandwidth-bound. Yet this evolution will shift the crossover point at which the more flop-intensive kernel using Cartesian expansions becomes competitive; we will then have the option of switching to this kernel for far-field calculations. Nevertheless, we are more optimistic than our colleagues about the hardware projections and think that architecture researchers will make a breakthrough before DGEMM is at risk of becoming memory-bound!
Another cause for optimism is the new spirit of collaboration emerging in the field. Leading up to the SIAM CSE conference, several groups were exchanging ideas about building a set of standard benchmark tests for FMM codes and, in due course, developing a community software library. A handful of open-source codes are already available, but adoption of multipole algorithms would thrive if we had a BLAS-like collection of highly optimized inner kernels for FMM and an FFTw-like auto-tuning framework that selects the best inner kernels for the application given the available hardware. An open collection of FMM kernels in a flexible framework would not only make it easy to compare various mathematical and implementation ideas, it would also promote collaboration and reduce duplication of efforts. Add to this a set of micro-benchmarks, a website that hosts the data sets and benchmark performance reports, and a mechanism for anyone to add a new data set or benchmark problem, and we would accelerate our collective pace.
The 2013 SIAM CSE conference was a milestone for the number of FMM researchers who came together in one place. On the basis of the handshakes and face-to-face conversations that took place in Boston, we may be ready to start building a virtual community for exascale FMM.
References
[1] A. Chandramowlishwaran, J.W. Choi, K. Madduri, and R. Vuduc, Brief announcement: Towards a communication optimal fast multipole method and its implications at exascale, Proceedings of the ACM Symposium on Parallel Algorithms and Architectures (SPAA), Pittsburgh, Pennsylvania, June 2012.
[2] M. Darbas, E. Darrigrand, and Y. Lafranche, Combining analytic preconditioner and fast multipole method for the 3-D Helmholtz equation, J. Comput. Phys., 236 (2012), 289–316.
[3] Z. Gimbutas and L. Greengard, Fast multiparticle scattering: A hybrid solver for the Maxwell equations in microstructured materials, J. Comput. Phys., 232:1 (2012), 22–32; preprint on http://arxiv.org/abs/1104.5293.
[4] K.L. Ho and L. Greengard, A fast direct solver for structured linear systems by recursive skeletonization, SIAM J. Sci. Comput., 34:5 (2012), A2507–A2532.
[5] H. Langston, L.F. Greengard, and D. Zorin, A freespace adaptive FMM-based PDE solver in three dimensions, Commun. Appl. Math. Comput. Sci., 6:1 (2011), 79–122.
[6] I. Lashuk, A. Chandramowlishwaran, H. Langston, T. Nguyen, R. Sampath, A. Shringarpure, R. Vuduc, L. Ying, D. Zorin, and G. Biros, A massively parallel adaptive fast-multipole method on heterogeneous architectures, Proceedings of the Conference on High Performance Computing, Networking, Storage, and Analysis, SC 2009, Portland, Oregon, 1–12; Commun. ACM, 55:5 (2012), 101–109; doi:10.1145/2160718.2160740.
[7] M. Winkel, R. Speck, H. Hübner, L. Arnold, R. Krause, and P. Gibbon, A massively parallel, multidisciplinary Barnes-Hut tree code for extreme-scale N-body simulations, Comput. Phys. Commun., 183:4 (2012), 880–889.
[8] R. Yokota and L.A. Barba, A tuned and scalable fast multipole method as a preeminent algorithm for exascale systems, Int. J. High-Perform. Comput. Applic., 2012; published online Jan. 24 (2012); doi:10.1177/1094342011429952; preprint on http://arxiv.org/abs/1106.2176.
[9] R. Yokota, L.A. Barba, T. Narumi, and K. Yasuoka, Petascale turbulence simulation using a highly parallel fast multipole method, Comput. Phys. Commun., 184:3 (2013), 445–455; preprint on arXiv:1106.5273.
[10] B. Zhang, B. Lu, X. Cheng, J. Huang, N.P. Pitsianis, X. Sun, and J.A. McCammon, Mathematical and numerical aspects of the adaptive fast multipole Poisson-Boltzmann solver, Commun. Comput. Phys., 13:1 (2013), 107–128.
Lorena A. Barba is an assistant professor in the Department of Mechanical Engineering at Boston University. Rio Yokota is a research scientist in the Strategic Initiative for Extreme Computing at KAUST in Saudi Arabia.