By Lakshmi Chandrasekaran
Have you ever wondered how an organism tries to solve a physiological problem on scales much larger than itself? For instance, humans construct architectures that are tens to hundreds of times bigger than themselves via a combination of systematic design, global planning, and effective communication between individuals.
How does this work for insects such as bees, wasps, termites, or ants, which tend to cohabitate in large colonies? To survive as a colony, social insects must solve some key problems, including maintaining mechanical stability, thermal regulation, and ventilation within the colony. “Here we see a fundamentally different approach to the solution, without a plan or a planner,” said L. Mahadevan, Lola England de Valpine Professor of Applied Mathematics, of Organismic and Evolutionary Biology, and of Physics at Harvard University. “Organisms respond to local rules and harness the environment to communicate information on scales much larger than themselves.” Building on earlier work pertaining to the thermoregulation of bee clusters [3] and active mechanical adaptation of bee swarms [4], Mahadevan’s group recently addressed the way in which a swarm of bees in a congested hive stays cool on hot summer days [5].
European honeybees (Apis mellifera) live in large, crowded enclosures with a single opening that limits passive ventilation. The colonies comprise more than 10,000 bees living together within tree hollows or other pre-existing cavities. These narrow, confined spaces present continuous survival challenges, including the need to maintain a stable temperature. This is especially true during extreme heat, when nest temperatures can reach a high of over 40° Celsius.
To understand how bees regulate colony temperatures, Jake Peters, now a postdoctoral fellow at Cornell University, monitored a group of artificial beehives housed at Harvard’s Concord Field Station. Figure 1a depicts the experiment, wherein a dense group of honeybees ventilates the hot box. The swarm creates an active fanning flow by moving to one side of the entrance and pulling hot air out of the hive. The other side of the entrance has few to no bees. Figure 1b shows that as the air temperature (red curve) increases along the nest entrance of a hive, the density of the fanning bees increases (black curve), as does the outward velocity of air (blue curve). The spatial patterning of the fanner bees yields a global convective flow that then cools the hive. But how do the bees spontaneously arrange themselves this way without a plan, especially since they start out by being uniformly distributed at the entrance?
Figure 1. Honeybee activity at a hive’s entrance. 1a. Honeybees ventilating at the entrance. There is a dense group of fanning bees at the left of the entrance and a dearth of fanning bees at the right. 1b. The air velocity (blue line), density (black line), and temperature (red line) along a hive’s nest entrance. Negative values indicate inflow while positive values indicate outflow. Figure courtesy of [5].
To explain this phenomenon, Mahadevan’s group hypothesized that the fanning bees use fluid flow to both measure the hive temperature and self-organize at the entrance. To understand the implications of this idea, the researchers created a mathematical model inspired by observations of the temperature, fluid flow, and fanner bee density along the colony’s entrance.
The model starts by characterizing the local fanning response of individual bees to the local air temperature, which is a proxy for the temperature inside the hive. “Indeed, by pulling the air out by fanning, the bees at the entrance can determine whether the nest needs to be cooled,” Mahadevan said. If it does, they recruit additional fanner bees that then work together to pull the hot air out. Mahadevan’s team links bee behavior, air temperature, and airflow by measuring how the distribution of fanning bees \(\rho (x, t)\), local air temperature \(T (x, t),\), and local flow velocity \(v (x, t)\) vary with time \(t\) along the nest entrance \(x\). Their model assumes that the local temperature determines the probability of a bee fanning at the entrance. The local density of fanning bees is given by
\[\frac{\partial \rho}{\partial t} = k_{\textrm{on}}(T) - k_{\textrm{off}}(T), \:\:\:\:\: \rho(x, t) \in [0, \rho_{\textrm{max}}], \tag1 \]
where \(k_\textrm{on}\) and \(k_\textrm{off}\) describe the rate at which bees begin or stop fanning behavior respectively. The maximum achievable density is represented by \(\rho_{\textrm{max}}\), which depends on space availability at the nest’s entrance.
The group modeled the fanning rates to describe the probability that a bee will fan at a given temperature via the following simple, switch-like sigmoidal function:
\[k_{\textrm{on}} = k_0 \frac{\tan h \big(m(T-36^{\circ} C)\big) + 1}{2} \tag2 \]
and
\[ k_{\textrm{off}} = k_0 - k_{\textrm{on}}. \tag3 \]
The parameter \(m\) determines the slope of the sigmoidal function that controls the temperature range over which bees ventilate. Since \(m\) is the model’s only behavioral parameter, Mahadevan and his colleagues hypothesize that natural selection has likely acted on the inter-individual variation in fanning thresholds. Such variation ensures efficient ventilation over the range of temperatures that the bees experience. Mahadevan compares the variable fanning threshold to slightly imperfect artificial temperature sensors in a building. “Having many sensors, each of which operates over a slightly different range of temperatures, collectively smooths out fluctuations in the environment and controls building temperature well,” he said. Similarly, subtle genetic variations—akin to the different sensors—confer different temperature thresholds in individual bees, above which they begin to fan. This mechanism enables bees to better react to temperature variations by responding to their individual local environments. Previous studies have shown that such diversity is essential to maintaining stable fanning behavior for efficient ventilation.
Mahadevan’s model then couples this fanning behavior to a minimal equation for fluid mass conservation across the hive entrance. To characterize the airflow, it assumes that each bee generates an outward airflow with velocity \(v_b\). Since the nest has only one opening, air that is actively drawn from the entrance must be balanced by air that flows into it to ensure conservation of mass. The following equation characterizes airflow in and out of the nest:
\[v (x, t) = l_b v_b \big[\rho (x, t) - \frac{1} {L} \int_0^L \rho(x,t)dx \big] + D_v \frac{\partial^2 v(x,t)}{\partial x^2}, \tag4\]
where \(v_b\) is the outward air flow generated by each bee. \(D_v\) indicates the scaled momentum diffusivity, \(L\) denotes the size of the nest length, and \(l_b\) represents the characteristic length scale derived from the fanning pressure gradient and fluid friction. The first term in (4) captures the outward airflow due to the actively fanning bees. However, this outflow must be balanced by inflow elsewhere, thus demanding the presence of a global inhibitor (second term) as it reverses flow direction and conserves the hive air volume. The last term represents local fluid friction and penalizes large velocity gradients (e.g., reversals in flow directions).
Finally, the researchers use a simple heat transfer equation that models temperature variation along the entrance, given by
\[\frac{\partial T(x, t)}{\partial t} = -cv(x, t) \Delta T + D_T \frac{\partial^2 T(x,t)}{\partial x^2}. \tag5 \]
Here, \(\Delta T =\begin{cases} T - T_h,\: \: if \: \: v \ge 0 \\ T_a - T,\: \: if \: \: v <0, \end{cases}\), and \(T_h\) and \(T_a\) are the hive and ambient temperatures respectively. Dimensionless forms of the equations reduce the number of parameters to just four: a scaled entrance size, a scaled thermal diffusivity, a scaled fluid friction parameter, and a scaled fanning bee size.
Interestingly, the form of equations \((1)\) through \((5)\) shows that fluid flow driven by bee recruitment follows a local excitation and global inhibition pattern. Fanning bees tend to excite other local fanners, while fluid conservation leads to long-range inhibition (see Figure 2). This collectively yields the emergent behavior observed in the field.
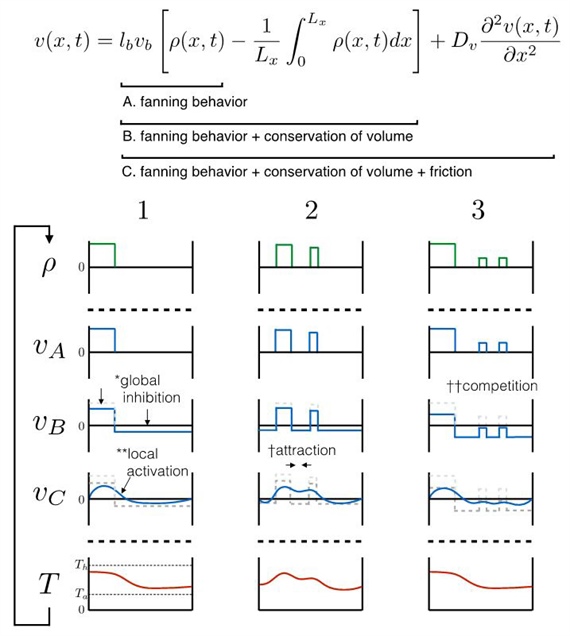
Figure 2. A schematic demonstrating the mechanisms of self-organization that emerge from the model. The fluid conservation equation is broken down into components: \(A\) is the direct result of fanning behavior, \(B\) is conservation of volume, and \(C\) is friction (or effective diffusion of velocity). The following variables are plotted: the distribution of fanners (\(\rho\)); velocity, calculated based only on fanning behavior (\(v_A\)); velocity, calculated based on fanning and conservation (\(v_B\)); velocity, calculated based on fanning, conservation, and friction (\(v_C\)); and temperature profile (\(T\)). Scenario 1 is a simple example that illustrates how volume conservation contributes to global inhibition of fanning behavior, and how fanning contributes to local activation. In other words, bees are more likely to fan adjacent to other fanning bees due to friction/diffusion. Scenario 2 illustrates a case in which friction/diffusion drives attraction between adjacent fanning groups. As a result, fanners are more likely to fan between fanning groups. Finally, Scenario 3 illustrates the potential for conservation of volume to act as a global inhibitor. Large fanning groups are more likely to grow and smaller groups are more likely to shrink and disappear due to this competition. Figure courtesy of [5].
Mahadevan and his collaborators numerically solved equations \((1)\) through \((5)\) to show that fanning behavior results in a clustering of the bees along one half of the nest’s entrance. This causes active outward flow of hot air where bees are present, and passive inward flow of cooler air everywhere else. Such behavior gives rise to a global convective flow that cools the hive. “Because of bees’ ability to measure local temperatures and fan to generate air flow—which then feeds back on their recruitment—this solution arises spontaneously,” Mahadevan said. The model’s predictions are qualitatively consistent with observations and show how fanning bees harness the dynamics of the physical environment and bring about self-organized behavior.
Studies like this one demonstrate how complex behavior in social insects can arise on large scales from simple local rules and long-range physical channels for communication, such as those induced by flow or elasticity. This type of work is quite distinct from the better-studied stigmergic mechanisms that rely on strongly localized communication channels, and has the potential for far-reaching implications [1]. For example, one could apply the insect ventilation problem to devise new strategies for passive and active sustainable human architecture [2].
Mahadevan co-authored this paper with Orit Peleg, a former postdoctoral fellow at Harvard who is now a faculty member at the University of Colorado, and Jake Peters, a former graduate student at Harvard who is now a postdoctoral fellow at Cornell University. Their work was supported by the National Science Foundation.
Acknowledgments: The author thanks L. Mahadevan for his time during the interview process and for his thorough review, feedback, and edits to this article.
References
[1] Heylighen, F. (2016) Stigmergy as a universal coordination mechanism. Cog. Syst. Res., 38, 4-13.
[2] Holbrook, C., Clark, R.M., Moore, D., Overson, R.P., Penick, C.A., & Smith, A.A. (2010). Social insects inspire human design. Bio. Lett., 6(4), 431-433.
[3] Ocko, S.A., & Mahadevan, L. (2014). Collective thermoregulation in bee clusters. J. Roy. Soc. Inter., 11(91), 20131033.
[4] Peleg, O., Peters, J., Salcedo, K., & Mahadevan, L. (2018). Collective mechanical adaptation of honeybee swarms. Nat. Phys., 14, 1193-98.
[5] Peters, J., Peleg, O., & Mahadevan, L. (2019). Collective ventilation in honeybee nests. J. Roy. Soc. Inter., 16(150), 20180561.
 |
Lakshmi Chandrasekaran received her Ph.D. in mathematical sciences from the New Jersey Institute of Technology. She earned her masters in science journalism from Northwestern University and is a freelance science writer whose work has appeared in several outlets. She can be reached on Twitter at @science_eye. |