By Sherry Towers, Oscar Patterson-Lomba, and Carlos Castillo-Chavez
Sir Ronald Ross introduced the first mathematical model for the transmission of malaria in 1911; this was the de facto creation of the field of mathematical epidemiology as we know it today. Kermack and McKendrick formulated the classic Susceptible, Infected, Recovered (SIR) compartmental model of the spread of disease in 1927. In the ensuing decades these models have been expanded in the broader context of host–parasite dynamics and disease evolution into the robust field of mathematical epidemiology [2, 7].
Soon after September 11, 2001, and the outbreak of Severe Acute Respiratory Syndrome in 2003, modelers across the world mobilized not only to forecast the progression of the SARS outbreak, but also to assess optimal control strategies, including quarantine and isolation (see, for instance, [4]), as well as the threats posed by the deliberate release of biological agents [1]. Identification of the causative agent responsible for SARS led to the quick development of diagnostic tools that, when combined with quarantine and isolation, were ultimately responsible for halting the spread of SARS. It was thus the efforts to assess the potential impact of SARS that highlighted the utility of single-outbreak epidemic models for emerging or re-emerging diseases.
The global health threat posed in 2009 by a pandemic influenza generated by a novel strain of A/H1N1 prompted further theoretical advances in modeling that led to a myriad of immediate and long-term contributions to our understanding of how to best control this global outbreak (see, for instance, [3, 8]). Most of these contributions involved assessing the rate of growth of an epidemic outbreak, estimation of its peak time, and the overall impact (final epidemic size). The models were also used to assess the role that interventions would have in reducing the peak, and to determine the conditions needed to turn a situation of explosive growth into one of no growth or decay.
The dimensionless quantity that plays a key role in assessing all the above factors with SIR Kermack–McKendrick-type models is known as the basic reproduction number, or \(R_0\) [2]. \(R_0\) measures the ability of a pathogen to invade a population not previously challenged by a disease, and the average number of secondary infections generated by a typical infectious individual introduced into a purely susceptible population. As time passes, in a closed population with constant transmission rate, the resource (susceptible individuals at time \(t\), \(S(t))\) becomes less accessible (because infected or recovered individuals are no longer susceptible). In other words, the rate of growth naturally begins to recede. Hence, the basic reproduction number \(R_0\) is distinguished from the effective reproduction number, \(R_e\), and \(R_e\) is sometimes modeled by a time-dependent dimensionless quantity \(R_{0}s(t)\), with \(s(t)\) being the proportion of susceptibles in the population at time \(t\). Finding ways of estimating appropriate measures for \(R_{e}(t)\) is critical to assessing the challenges posed by emergent or re-emergent diseases over short times.
The West African Ebola outbreak has inspired several new modeling analyses, motivated by our desire to contribute to the understanding of the dynamics underlying this emerging global health threat. The 2014 Ebola outbreak is characterized by rapidly changing local and regional dynamics, altered by evolving control measures, patterns of spread from rural to densely populated urban areas [5], and behavioral responses in the population that may either inhibit or facilitate the spread of the disease [6]. Therefore, it is evident that the design of real-time control strategies must include temporal components that capture the unfolding dynamics and the variable transmission rate of Ebola.
Our recent paper “Temporal Variations in the Effective Reproduction Number of the 2014 West Africa Ebola Outbreak” makes use of the limited existing data and novel elementary statistical methods (in this context), in combination with a simple single-epidemic nonlinear dynamic model and its associated \(R_e\), to determine whether the transmission rate of Ebola has been changing over time in West Africa [9]. To this end, piecewise exponential curves were fit to the time series of outbreak data (see Figure 1). This ansatz, combined with a mathematical model, was used to estimate the temporal evolution of the effective reproduction number of the disease, estimating the temporal variations in the average number of secondary cases per infectious case in a population composed of both susceptible and non-susceptible individuals. Typically, depletion of susceptible individuals in a closed population during the course of an outbreak would cause the effective reproduction number to decline over time, with a faster-than-expected drop suggesting that control measures and/or changes in population behaviors are effective in inhibiting the spread of the disease. Accordingly, an increasing \(R_e\) would indicate a worsening of the conditions.
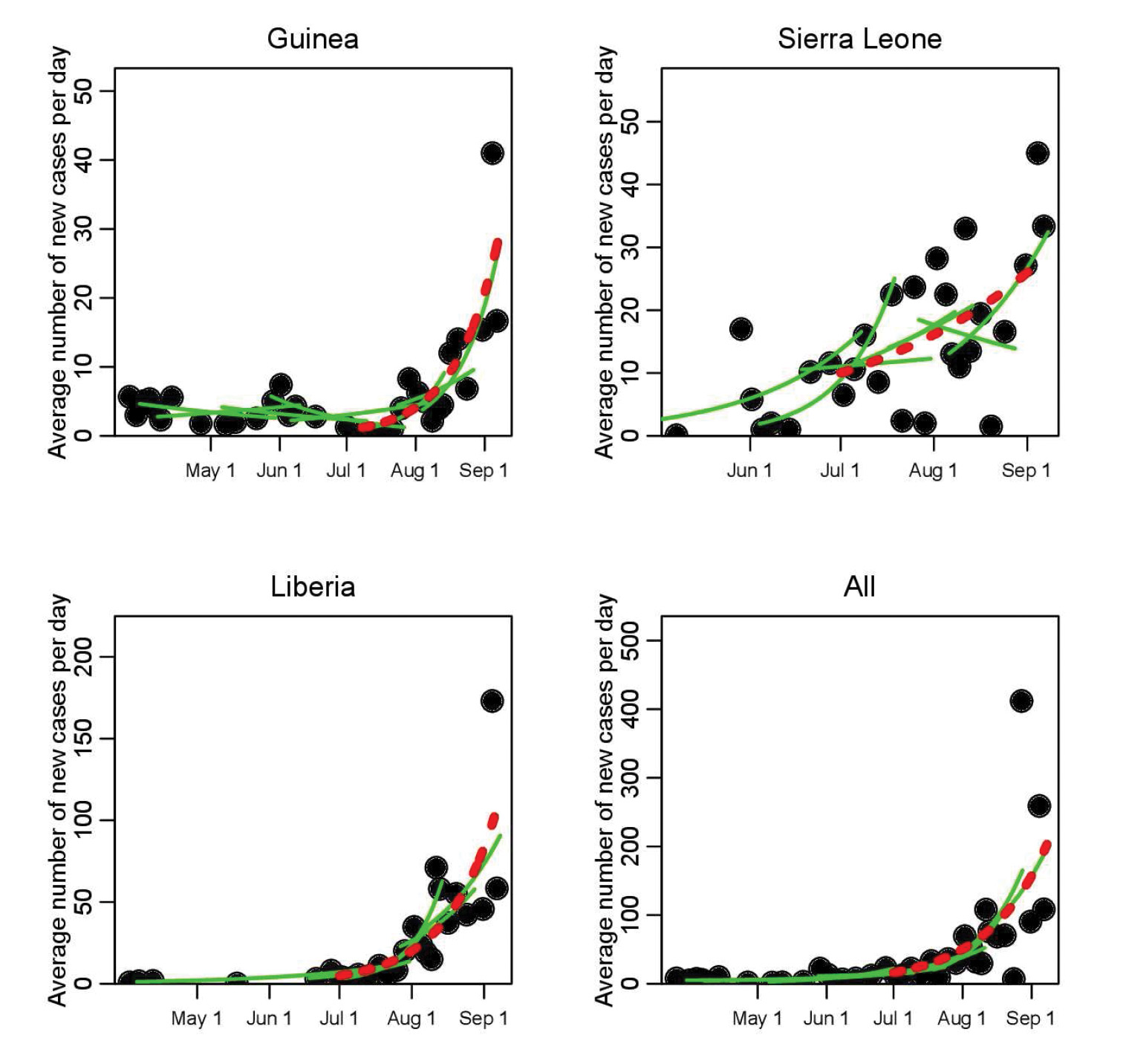
Figure 1. Time series of recorded average number of new Ebola Virus Disease cases per day during the initial phase of the 2014 West African outbreak, for Guinea, Sierra Leone, and Liberia (dots). The green lines show a selection of the piecewise exponential fits to the data (for clarity of the presentation, not all fits are shown); a moving window takes groups of 10 contiguous points at a time, and the rate of exponential rise (or decline) is estimated for those 10 points. As a reference, the red dotted line shows the fit to all points between July 1 and September 8, 2014. The results for the estimated exponential rise for the full set of piecewise fits are shown in Figure 2.
|
Unfortunately, yet not surprisingly, rather than a drop in the effective reproduction number, our study showed evidence that the transmission rate of Ebola in Guinea and Liberia actually rose in early August (see Figure 2). What led to the increased transmission rate is somewhat unclear, as many factors could be responsible. Was it increases in the size of the susceptible population linked to the time when the outbreak spread to densely populated cities? Or was it the military-enforced quarantine of entire regions in West Africa, measures that were put in place with no attempt to limit the spread of disease within the quarantined areas, and that may thus have increased the risk of transmission due to crowding, lack of medical and basic services, and poor sanitation? If the latter, then it is clear that careful attention must be paid to the design of control measures to ensure that they, first and foremost, do no harm. The analysis further indicated that if the exponential growth in the spread continued, there would have been approximately 4400 new Ebola cases by the beginning of October (95% confidence interval [3000,6800]). Unfortunately, the actual case counts by that date were within the predicted range.
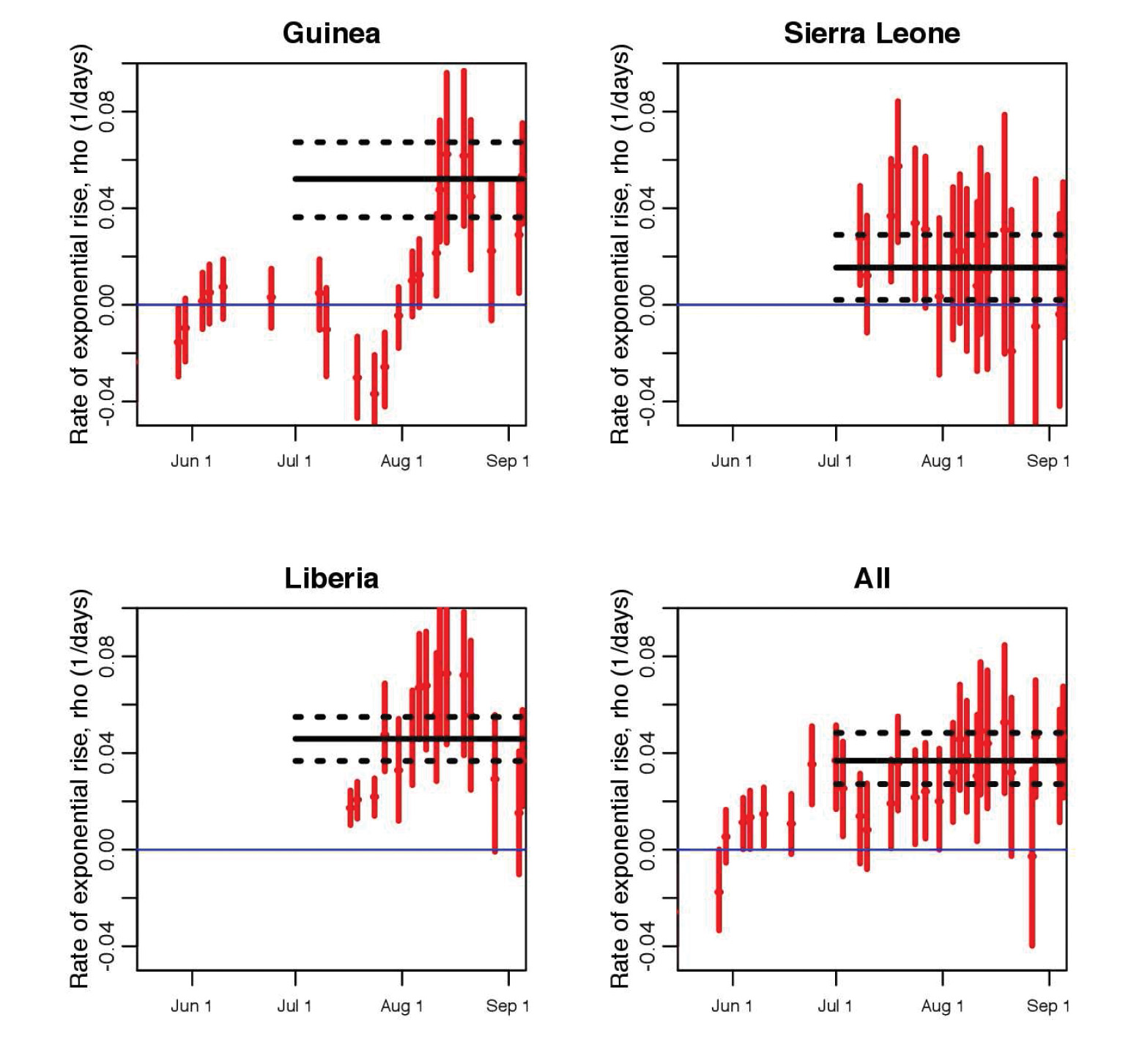
Figure 2. Estimated exponential rise from piecewise exponential fits to the average daily EVD incidence data, as shown in Figure 1; a moving window takes groups of 10 contiguous incidence data time series points at a time, and the rate of exponential rise is estimated for those 10 points. The dates shown on the x-axis are the last date in each contiguous set of 10 points, and the vertical error bars denote the 95% confidence interval. The horizontal black line shows the estimated rate of rise of an exponential fit to the incidence time series from July 1 to the present, with the black dotted lines indicating the 95% interval. |
Beyond its applicability to the current Ebola outbreak, this data-driven approach gives public health experts a simple framework that is useful for assessing in near-real time whether control efforts are efficacious.
References
[1] H.T. Banks and C. Castillo-Chavez, eds., Bioterrorism: Mathematical Modeling Applications in Homeland Security, SIAM, Philadelphia, 2003.
[2] F. Brauer and C. Castillo-Chavez, Mathematical Models in Population Biology and Epidemiology, Springer, New York, 2001.
[3] C. Castillo-Chavez and G. Chowell, Mathematical models, challenges and lessons learned from the 2009 A/H1N1 influenza pandemic, Math. Biosci. Eng., 8:1 (2011).
[4] G. Chowell, P.W. Fenimore, M.A. Castillo-Garsow, and C. Castillo-Chavez, SARS outbreaks in Ontario, Hong Kong and Singapore: The role of diagnosis and isolation as a control mechanism, J. Theoret. Biol., 224:1 (2003), 1–8.
[5] M.C.M. de Jong, O. Diekmann, and H. Heesterbeek, How does transmission of infection depend on population size? Epidemic Models: Their Structure and Relation to Data, 5:2 (1995), 84–94.
[6] E.P. Fenichel, C. Castillo-Chavez, M.G. Ceddia, G. Chowell, P.A. Gonzalez Parra, G.J. Hickling, G. Holloway, R. Horan, B. Morin, C. Perrings, et al., Adaptive human behavior in epidemiological models, Proc. Natl. Acad. Sci. USA, 108:15 (2011), 6306–6311.
[7] H.W. Hethcote, The mathematics of infectious diseases, SIAM Rev., 42:4 (2000), 599–653.
[8] S. Towers and Z. Feng, Pandemic H1N1 influenza: Predicting the course of a pandemic and assessing the efficacy of the planned vaccination programme in the United States, Euro Surveill., 14:41 (2009), 19358.
[9] S. Towers, O. Patterson-Lomba, and C. Castillo-Chavez, Temporal variations in the effective reproduction number of the 2014 West Africa Ebola Outbreak, PLoS Currents: Outbreaks, 1, 2014.
Sherry Towers is a research professor at the Simon A. Levin Mathematical, Computational, and Modeling Sciences Center at Arizona State University. Oscar Patterson-Lomba is a postdoctoral research fellow at the Harvard School of Public Health. Carlos Castillo-Chavez is the Joaquin Buston, Jr. Professor of Mathematical Biology and a Distinguished Sustainability Scientist at Arizona State University.