By Shinnosuke Seki
Transcription is a process that synthesizes a temporal copy of a gene—called a transcript—out of an RNA molecule. The transcript acts as an intermediary to express a protein or non-coding RNA encoded in the gene. A gene is a chemically-directed chain of deoxyribonucleotides \(\textrm{A}\), \(\textrm{C}\), \(\textrm{G}\), and \(\textrm{T}\). The synthesis proceeds sequentially. An enzyme called RNA polymerase scans a gene unidirectionally and binds one ribonucleotide of the type (\(\textrm{A}\), \(\textrm{C}\), \(\textrm{G}\), or \(\textrm{U}\)) most energetically preferred by what is read to the growing transcript; the preference is \(\textrm{A} \rightarrow \textrm{U}\), \(\textrm{C} \rightarrow \textrm{G}\), \(\textrm{G} \rightarrow \textrm{C}\), and \(\textrm{T} \rightarrow \textrm{A}\). Upon further modification, the transcript may adopt a precise tertiary structure (conformation), thus allowing it to perform its function.
Some modifications, such as the removal of introns (splicing) from a transcript, are cotranscriptional: as transcription occurs, introns fold into a loop and are excised. Cotranscriptional folding occurs when a transcript folds upon itself during synthesis. Such folding is possible because transcripts fold considerably faster than they synthesize. The relative speed of folding to synthesis seems to be predetermined in nature, but the reason for this is unknown. Indeed, computation of thermodynamics indicates that polymerase deceleration could save energy [3]. The specific transcription rate and directionality of synthesis enable nature to “program” a gene’s biological function [8], with polymerase as a compiler from the genetic “source code” back to the executable program, that is, biological function. The source code offers inheritability to nature and readability to us.
In 2014, Cody Geary, Paul Rothemund, and Ebbe Andersen exhibited a command of this programming language as RNA origami [5], fabricating complicated shapes—such as rectangular tiles—from RNA molecules (see Figure 1). The tile hinges its left and right halves—each of which is a stratus of hairpins, i.e., strong double-helical stems ending in a loop—at the bottom. First, the left half cotranscriptionally folds through a pathway of events to form the hairpins, then the right half folds as such and is stapled cotranscriptionally to the folded left half. The two halves are held together weakly via paranemic “kissing” loops (see Figure 2). By the time the right half begins undergoing synthesis, the left has already been constrained too strictly to form a strong double-helical segment with the right.
Figure 1. RNA origami. The transcript (blue) folds into a rectangular tile while being synthesized by the RNA polymerase (orange). Image courtesy of [5].
RNA origami will likely be the “Hello, World!” of future educational materials on the programming of cotranscriptional folding: a symbolic and static code that always behaves consistently. Readers will then move to chapters on more dynamic codes for information processing. The oritatami system is a mathematical model recently proposed by Geary, Pierre-Étienne Meunier, Nicolas Schabanel, and myself to establish theoretical grounds for these chapters [4]. As shown in Figure 2, the oritatami system abstracts a conformation as a directed, vertex-labeled path (transcript) on the triangular grid with bonds between adjacent vertices. Vertices on the path are called beads. A bead may represent one nucleotide or a region of consecutive nucleotides depending on the abstraction level, and its label is taken from an alphabet \(\Sigma\) of bead types. For \(x, y \in \Sigma\), an \(x\)-bead can bind with a \(y\)-bead only if the pair \((x,y)\) belongs to the rule set \(\mathcal{H}\), a symmetric relation in \(\Sigma^2\). Two other parameters exist: the delay \(\delta\) abstracts the transcription rate and the arity \(\alpha\) bounds the number of bonds that one bead can form. An oritatami system is a tuple \((\Sigma, w, \mathcal{H}, \delta, \alpha, \sigma)\). Upon its initial “seed” conformation \(\sigma\), the system transcribes the first \(\delta\) beads of its transcript \(w \in \Sigma^*\) and repeats the following instructions until the end of \(w\):
- Fold the fragment of nascent beads to elongate the current conformation with as many new bonds as possible.
- Stabilize the eldest nascent bead with all its bonds accordingly.
- Transcribe the next bead, if any.
Figure 2. Abstraction of the RNA tile structure as a conformation in an oritatami system. The dashed lines indicate bonds. Left image courtesy of Cody Geary, right image courtesy of Shinnosuke Seki.
The oritatami system thus folds its transcript \(w\) cotranscriptionally. Figure 3 depicts a delay-3 oritatami system folding a rigid directional structure motif nicknamed glider. Any bead or its absence outside the circle of radius \(\delta + 1\) centered at the last bead stabilized cannot affect the fragment of nascent beads. In this sense, the circle is called the event horizon or context.
In computing, it seems essential for oritatami systems to refer to some kind of “memory.” Random access is one of the most essential capabilities for computation, and most computational models are either equipped with a random-access memory or capable of readily implementing it. The former is not the case for oritatami systems. Regardless of the transcript’s prior folding, subsequent transcription is predetermined by \(w\) and does not change. Oritatamists have therefore speculated that the only plausible way for oritatami systems to “remember” is to equip a transcript with the capability of sensitively folding into more than one conformation to multiple possible event horizons.
Two possible event horizons and corresponding conformations may carry \(1\)-bit information.
This turned out to be the central principle in designing an oritatami binary counter [4]. Its transcript is periodic as 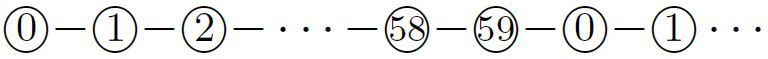 of period \(60\), where integers represent bead types. The periodically-occurring factor
of period \(60\), where integers represent bead types. The periodically-occurring factor 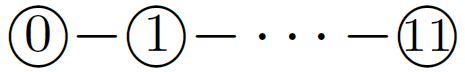 along the transcript is called a half-adder module. The transcript folds cotranscriptionally upon the seed shown in Figure 4 (top). The event horizons that the first two occurrences of the factor encounter are distinct enough to favor different conformations, (see Figure 4, middle and bottom). The rule set of the system is designed carefully so as to equip the half-adder module with the capability of folding into four conformations, depending on the sequence of the four bead types above, which encodes a \(1\)-bit input, and on whether a module starts folding at the top (carry = \(0\)) or bottom (carry = \(1\)). These four conformations expose different sequences of bead types distinguishable enough to encode a \(1\)-bit output, and place its last bead (of type \(11\)) at the top or bottom to represent a carry. For instance, the event horizon encountered by the first half-adder module feeds \(0\) with carry to the module and causes the module to fold so as to output \(1\) without carry, while the event horizon for the second feeds \(0\) without carry and folds the module so as to output \(0\) without carry. Two event horizons encoding \(1\) with or without carry fold a half-adder module into one of the other two possible conformations, respectively. The system is designed such that half-adders never encounter any other unexpected event horizon.
along the transcript is called a half-adder module. The transcript folds cotranscriptionally upon the seed shown in Figure 4 (top). The event horizons that the first two occurrences of the factor encounter are distinct enough to favor different conformations, (see Figure 4, middle and bottom). The rule set of the system is designed carefully so as to equip the half-adder module with the capability of folding into four conformations, depending on the sequence of the four bead types above, which encodes a \(1\)-bit input, and on whether a module starts folding at the top (carry = \(0\)) or bottom (carry = \(1\)). These four conformations expose different sequences of bead types distinguishable enough to encode a \(1\)-bit output, and place its last bead (of type \(11\)) at the top or bottom to represent a carry. For instance, the event horizon encountered by the first half-adder module feeds \(0\) with carry to the module and causes the module to fold so as to output \(1\) without carry, while the event horizon for the second feeds \(0\) without carry and folds the module so as to output \(0\) without carry. Two event horizons encoding \(1\) with or without carry fold a half-adder module into one of the other two possible conformations, respectively. The system is designed such that half-adders never encounter any other unexpected event horizon.
Figure 4. An oritatami binary counter. Image courtesy of [4].
Due to further developments, an oritatami system to simulate a cyclic tag system is now nearly complete. The cyclic tag system is capable of simulating a Turing machine [2], and the cyclic tag system simulator would prove that the oritatami system is Turing-universal, that is, capable of computing all computable functions. Innovative features of the simulator include cyclically-accessible memory, transcription-halting machinery, geometrical “hill-and-dale” encoding, and the glider. Turing-universality marks the first key milestone, suggesting implementability of artificial inheritable stored-program computers.
With hope and the meager tools invented thus far, oritatamists venture into the frontier of cotranscriptional folding. The next milestone is intrinsic universality, the capability of one oritatami system to mimic the behavior of an arbitrary other. An intrinsically-universal oritatami system would offer a prototype of a universal programming language for RNA cotranscriptional folding. It seems quite distant, though, and there are many problems to be settled. The oritatami system discards some kinetic and topological details of RNA cotranscriptional folding to shed light on its computational aspects. Expertise and insights from diverse fields such as RNA kinetics, molecular dynamics, and topology would complement the oritatami system and consolidate theory and experiments into an in-vivo execution of basic computational steps by RNA cotranscriptional folding.
Acknowledgments: This work is in part supported by JST Program to Disseminate Tenure Tracking System No. 6F36 and JSPS KAKENHI Grant-in-Aid for Young Scientists (A) No. 16H05854. The author appreciates Cody Geary, Yo-Sub Han, Hwee Kim, Trent Rogers, Miyako Satoh, and Nicolas Schabanel for their valuable comments on earlier versions of this article.
References
[1] Beyer, A.L., Bouton, A.H., & Miller Jr., O.L. (1981). Correlation of hnRNP structure and nascent transcript cleavage. Cell, 26(2), 155-165.
[2] Cook, M. (2004). Universality in elementary cellular automata. Complex Systems, 15, 1-40.
[3] Feynman, R.P. (1996). Feynman Lectures on Computation. Cambridge, MA: Perseus Books Group.
[4] Geary, C., Meunier, P.-É., Schabanel, N., & Seki, S. (2016). Programming biomolecules that fold greedily during transcription. In Proc. 41st International Symposium on Mathematical Foundations of Computer Science (MFCS 2016). Vol. 58 of Leibniz International Proceedings in Informatics (pp. 43:1-43:14).
[5] Geary, C., Rothemund, P.W.K., & Andersen, E.S. (2014). A single-stranded architecture for cotranscriptional folding of RNA nanostructures. Science, 345, 799-804.
[6] Merkhofer, E.C., Hu, P., & Johnson, T.L. (2014). Introduction to cotranscriptional RNA splicing. In K.J. Hertel (Ed.), Spliceosomal Pre-mRNA Splicing: Methods and Protocols (pp. 83-96). Vol. 1126 of Methods in Molecular Biology, New York, NY: Springer.
[7] Wu, Z., Murphy, C., Callan, H.G., & Gall, J.G. (1991). Small nuclear ribonucleoproteins and heterogeneous nuclear ribonucleoproteins in the amphibian germinal vesicle: Loops, spheres, and snurposomes. Journal of Cell Biology, 113(3), 465-483.
[8] Xayaphoummine, A., Viasnoff, V., Harlepp, S., & Isambert, H. (2007). Encoding folding paths of RNA switches. Nucleic Acids Res., 35(2), 614-622.
Shinnosuke Seki is an assistant professor in the Department of Computer and Network Engineering at the University of Electro-Communications in Tokyo, Japan. His research interests are in theoretical and computational models of molecular self-assembly.